

Final Programación Concurrente
Finales de la materia programación concurrente

📌 Preguntas Practicas FIJAS
- 1) Calculos con Matrices
- 2) Cuales Cumplen con ASV
- 3) Cuales Cumplen con ASV 2
- 4) Numero de Mensajes y Granularidad
- 5) Numero de Mensajes y Granularidad 2
- 6) Indicar para cada item si son equivalentes
- 7) ¿Que valores quedan?
- 8) ¿Que valores quedan? 2
- 9) La Solución a un problema es paralelizada
- 10) La Solución a un problema es paralelizada 2
- 11) La Solución a un problema es paralelizada 3
- 12) La Solución a un problema es paralelizada 4
- 13) Suponga que el tiempo de ejecución de un algoritmo Secuencial
- 14) Suponga que el tiempo de ejecución de un algoritmo Secuencial 2
- 15) Suponga que el tiempo de ejecución de un algoritmo Secuencial 3
- 16) Calcular la suma de todos los valores
- 17) Token passing con mensajes asincrónicos
📢 Miralas de Reojo
- 1) Propuesta al problema de alocación SJN
- 2) “passing the condition” En Semaforos
- 3) Problema de Concurrencia
- 4) Problema de Concurrencia 2
- 5) Indique los posibles valores finales de x
- 6) Cuales valores de k son posibles
🚨 Rezar para que no Tomen
- 1) Resuelva con monitores
- 2) Protocolos de Acceso a la SC
- 3) Solución a la Criba
- 4) Transformar Solucion usando mensajes asincronicos
- 5) Problema de ordenar de menor a mayor un arreglo
- 6) Problema de ordenar de menor a mayor 2
- 7) Suponga que un proceso productor y
nprocesos consumidores - 8) Implemente una butterfly barrier para 8 procesos
- 9) Suponga n^2 procesos organizados en forma de grilla cuadrada
- 10) Una imagen se encuentra representada por una matriz
Notas#






















Aprendes o te moris#
0) Una imagen se encuentra representada por una matriz#
Suponga que una imagen se encuentra representada por una matriz a (n×n), y que el valor de cada pixel es un número entero que es mantenido por un proceso distinto (es decir, el valor del píxel I,J está en el proceso P(I,J)). Cada proceso puede comunicarse solo con sus vecinos izquierdo, derecho, arriba y abajo. (Los procesos de las esquinas tienen solo 2 vecinos, y los otros bordes de la grilla tienen 3 vecinos).
a) Escriba un algoritmo Herbeat que calcule el máximo y el mínimo valor de los píxeles de la imagen. Al terminar el programa, cada proceso debe conocer ambos valores.
chan topologia[1:n](
proceso_emisor : int;
ya_conoce_todo : bool;
topologia_conocida : [1:n,1:n] bool;
valor_max : int;
valor_min : int
);
process nodo[p = 1..n] {
bool vecinos_directos[1:n]; # inicialmente vecinos[q] true si q es vecino de p
bool vecinos_activos[1:n] = vecinos_directos; # vecinos aún activos
bool topologia_conocida[1:n,1:n] = ([n*n]false); # vecinos conocidos (matriz de adyacencia)
bool topologia_recibida[1:n,1:n];
bool ya_conoce_todo = false;
int proceso_emisor;
bool vecino_listo;
int valor_pixel_local, valor_max, valor_min;
topologia_conocida[p,1..n] = vecinos_directos; # llena la fila para los vecinos
valor_max := valor_pixel_local;
valor_min := valor_pixel_local; # miValor inicializado con el valor del píxel
while (not ya_conoce_todo) { # envía conocimiento local de la topología a sus vecinos
for (vecino = 1 to n st vecinos_activos[vecino]) {
send topologia[vecino](p, false, topologia_conocida, valor_max, valor_min);
}
for (vecino = 1 to n st vecinos_activos[vecino]) {
receive topologia[p](proceso_emisor, vecino_listo, topologia_recibida, nuevoMax, nuevoMin);
topologia_conocida = topologia_conocida or topologia_recibida; # hace OR con su top juntando la información
if (nuevoMax > valor_max) valor_max := nuevoMax; # actualiza los máximos y mínimos
if (nuevoMin < valor_min) valor_min := nuevoMin;
if (vecino_listo) vecinos_activos[proceso_emisor] = false;
}
if (todas las filas de topologia_conocida tienen 1 entry true) ya_conoce_todo = true;
}
# envía topología completa a todos sus vecinos aún activos
for (vecino = 1 to n st vecinos_activos[vecino]) {
send topologia[vecino](p, ya_conoce_todo, topologia_conocida, valor_max, valor_min);
}
# recibe un mensaje de cada uno para limpiar el canal
for (vecino = 1 to n st vecinos_activos[vecino]) {
receive topologia[p](proceso_emisor, ya_conoce_todo, topologia_recibida, nuevoMax, nuevoMin);
}
}Esto se tiene que consultar, porque la solución es mucho mas simple de la que esta aca
b) Analice la solución de desde el punto de vista del número de mensajes.
Si M es el numero maximo de vecinos que puede tener un nodo, y D es el diametro de la red, el número de mensajes maximo que pueden intercambiar es de 2n * m * (D+1). Esto es porque cada nodo ejecuta a lo sumo D-1 rondas, y en cada una de ellas manda 2 mensajes a sus m vecinos
1) Calcular la suma de todos los valores#
Suponga que N procesos poseen inicialmente cada uno un valor. Se debe calcular la suma de todos los valores y al finalizar la computación todos deben conocer dicha suma.
Analice (desde el punto de vista del número de mensajes y la performance global) las soluciones posibles con memoria distribuida para arquitecturas en Estrella (centralizada), Anillo Circular, Totalmente Conectada y Árbol.
arquitecturas en Estrella(centralizada)
En este tipo de arquitectura todos los procesos (workers) envían su valor local al procesador central (coordinador), este suma los N datos y reenvía la información de la suma al resto de los procesos.
Por lo tanto se ejecutan 2(N-1) mensajes. Si el procesador central dispone de una primitiva broadcast, se reduce a N mensajes.
En cuanto a la performance global, los mensajes al coordinador se envían casi al mismo tiempo.
Estos se quedarán esperando hasta que el coordinador termine de computar la suma y envíe el resultado a todos.
chan canal_valor(INT);
canal_resultado[n](INT suma);
Process Coordinador[0]{ // coordinador, v está inicializado
INT valor_local;
INT suma_total = 0;
suma_total = suma_total + valor_local;
for (i = 1 to n-1){
receive canal_valor(valor_recibido);
suma_total = suma_total + valor_recibido;
}
for (i = 1 to n-1)
send canal_resultado[i](suma_total);
}
process Trabajador[i = 1 to n-1]{ // worker, v está inicializado
INT valor_local;
INT suma_total;
send canal_valor(valor_local);
receive canal_resultado[i](suma_total);
}🧩 Supuestos
De nuevo usamos n = 4 procesos:
| Proceso | Rol | Valor local v[i] |
|---|---|---|
| P[0] | Coordinador | 2 |
| P[1] | Worker | 3 |
| P[2] | Worker | 5 |
| P[3] | Worker | 7 |
🎯 Objetivo
P[0]recibe los valores de todos los procesos.- Suma:
2 + 3 + 5 + 7 = 17. - Luego envía la suma global de vuelta a todos los workers.
🚀 Ejecución paso a paso
📨 Fase 1: Envío de los valores al coordinador
| Paso | Acción |
|---|---|
| 1 | P[1] envía 3 a P[0] |
| 2 | P[2] envía 5 a P[0] |
| 3 | P[3] envía 7 a P[0] |
| 4 | P[0] ya tiene su v = 2, recibe 3, 5, y 7, suma total = 17 |
📤 Fase 2: Coordinador difunde la suma
| Paso | Acción |
|---|---|
| 5 | P[0] envía 17 a P[1] |
| 6 | P[0] envía 17 a P[2] |
| 7 | P[0] envía 17 a P[3] |
✅ Resultado final
| Proceso | Valor final conocido |
|---|---|
| P[0] | 17 (lo calculó) |
| P[1] | 17 (lo recibió) |
| P[2] | 17 (lo recibió) |
| P[3] | 17 (lo recibió) |
💬 Observaciones
- Total de mensajes:
2(n - 1)=2(4 - 1)= 6 mensajes - Con broadcast: solo
n = 4mensajes (1 de cada worker al coordinador, 1 broadcast de vuelta). - Buena performance en tiempo, porque los workers envían todos al mismo tiempo.
- Pérdida de paralelismo en el cómputo: solo el coordinador trabaja, los demás esperan.
- Punto único de falla: si
P[0]se cae, el sistema no funciona.
Anillo circular
Se tiene un anillo donde P[i] recibe mensajes de P[i-1] y envía mensajes a P[i+1]. P[n-1] tiene como sucesor a P[0]. El primer proceso envía su valor local ya que es el único que conoce.
Este esquema consta de dos etapas:
- Cada proceso recibe un valor y lo suma con su valor local, transmitiendo la suma local a su sucesor.
- Todos reciben la suma global.
P[0] debe ser algo diferente para poder “arrancar” el procesamiento: debe enviar su valor local ya que es el único que conoce. Se requerirán 2(n-1) mensajes.
A diferencia de la solución centralizada, esta reduce los requerimientos de memoria por proceso pero tardara más en ejecutarse, por más que el número de mensajes requeridos sea el mismo. Esto se debe a que cada proceso debe esperar un valor para computar una suma parcial y luego enviársela al siguiente proceso; es decir, un proceso trabaja por vez, se pierde el paralelismo.
chan canal_suma[n](suma_parcial);
process p[0] {
INT valor_local;
INT suma_parcial = valor_local;
send canal_suma[1](suma_parcial);
receive canal_suma[0](suma_parcial);
send canal_suma[1](suma_parcial);
}
process ProcesoAnillo[i = 1 to n-1] {
INT valor_local;
INT suma_parcial;
receive canal_suma[i](suma_parcial);
suma_parcial = suma_parcial + valor_local;
siguiente = (i + 1) mod n
send canal_suma[siguiente](suma_parcial);
receive canal_suma[i](suma_parcial);
if (i < n - 1)
send canal_suma[i + 1](suma_parcial);
}| Proceso | v[i] |
|---|---|
| P[0] | 2 |
| P[1] | 3 |
| P[2] | 5 |
| P[3] | 7 |
El objetivo es que todos los procesos conozcan la suma total, que es 2 + 3 + 5 + 7 = 17.
🧠 Etapa 1: Suma parcial hacia adelante
| Paso | Acción |
|---|---|
| 1 | P[0] envía 2 a P[1] |
| 2 | P[1] recibe 2, suma su v=3, total = 5, envía 5 a P[2] |
| 3 | P[2] recibe 5, suma su v=5, total = 10, envía 10 a P[3] |
| 4 | P[3] recibe 10, suma su v=7, total = 17, envía 17 a P[0] |
🧠 Etapa 2: Difusión de la suma global
| Paso | Acción |
|---|---|
| 5 | P[0] recibe 17 de P[3], reenvía 17 a P[1] |
| 6 | P[1] recibe 17, reenvía 17 a P[2] |
| 7 | P[2] recibe 17, reenvía 17 a P[3] |
| 8 | P[3] recibe 17 |
✅ Resultado final
Todos los procesos conocen el valor total 17.
| Proceso | Valor recibido |
|---|---|
| P[0] | 17 |
| P[1] | 17 |
| P[2] | 17 |
| P[3] | 17 |
💬 Observaciones
- Cantidad de mensajes: 2(n - 1) = 2(4 - 1) = 6 mensajes, como indica tu descripción.
- Secuencialidad: cada proceso espera su turno para sumar → no hay paralelismo.
- P[0] es especial, porque inicia la suma y también es el primero que difunde la suma global.
Totalmente conectada (simetrica)
Todos los procesos ejecutan el mismo algoritmo. Existe un canal entre cada par de procesos.
Cada uno transmite su dato local v a los n-1 restantes. Luego recibe y procesa los n-1 datos que le faltan, de modo que en paralelo toda la arquitectura está calculando la suma total y tiene acceso a los n datos.
Se ejecutan n(n-1) mensajes. Si se dispone de una primitiva de broadcast, serán n mensajes.
Es la solución más corta y sencilla de programar, pero utiliza el mayor número de mensajes si no hay broadcast.
chan canal_valor[n](INT);
process Proceso[i=0 to n-1] {
INT valor_local;
INT valor_recibido
INT suma_total = valor_local;
for (int destino = 0 to n-1 st destino <> i)
send canal_valor[destino](valor_local);
for (int origen = 0 to n-1 st k <> i) {
receive canal_valor[i](valor_recibido);
suma_total = suma_total + valor_recibido;
}
}🧩 Supuestos
Usamos de nuevo n = 4 procesos y valores locales:
| Proceso | v[i] |
|---|---|
| P[0] | 2 |
| P[1] | 3 |
| P[2] | 5 |
| P[3] | 7 |
🚀 ¿Qué hace cada proceso?
- Cada proceso envía su valor a los otros 3 (
n-1). - Luego, recibe los 3 valores que le faltan, y los suma.
- Esto se hace en paralelo, es decir, todos los procesos trabajan al mismo tiempo.
📊 Ejecución paso a paso
Fase 1: Envío
| Proceso | Envía a… | Mensajes |
|---|---|---|
| P[0] | P[1], P[2], P[3] | 3 |
| P[1] | P[0], P[2], P[3] | 3 |
| P[2] | P[0], P[1], P[3] | 3 |
| P[3] | P[0], P[1], P[2] | 3 |
| Total | 12 mensajes |
Fase 2: Recepción y suma
Cada proceso recibe 3 valores y los suma con el propio:
| Proceso | Valores recibidos | Suma final |
|---|---|---|
| P[0] | 3, 5, 7 | 2 + 3 + 5 + 7 = 17 |
| P[1] | 2, 5, 7 | 3 + 2 + 5 + 7 = 17 |
| P[2] | 2, 3, 7 | 5 + 2 + 3 + 7 = 17 |
| P[3] | 2, 3, 5 | 7 + 2 + 3 + 5 = 17 |
✅ Resultado final
Todos conocen la suma global 17.
| Proceso | Suma calculada |
|---|---|
| P[0] | 17 |
| P[1] | 17 |
| P[2] | 17 |
| P[3] | 17 |
💬 Observaciones
- Total de mensajes:
n(n-1)=4 × 3= 12 mensajes - Todos trabajan en paralelo → alta velocidad
- Pero: requiere muchos canales y mensajes
- Si tuvieras broadcast, solo necesitarías n mensajes (1 por proceso).
Arbol
Se tiene una red de procesadores (nodos) conectados por canales de comunicación bidireccionales. Cada nodo se comunica directamente con sus vecinos. Si un nodo quiere enviar un mensaje a toda la red, debería construir un árbol de expansión de la misma, poniéndose a él mismo como raíz.
El nodo raíz envía un mensaje por broadcast a todos los hijos, junto con el árbol construido. Cada nodo examina el árbol recibido para determinar los hijos a los cuales deben reenviar el mensaje, y así sucesivamente.
Se envían n - 1 mensajes, uno por cada padre/hijo del árbol.
🧩 Supuestos
- Tenemos
n = 7nodos numerados del0al6. - Se construye un árbol de expansión para propagar un mensaje, con el nodo
0como raíz. - El árbol tiene esta estructura (por simplicidad):
0
/ | \
1 2 3
| \
4 5
\
6🎯 Objetivo
Difundir un mensaje desde el nodo raíz (0) hacia todos los demás nodos usando el árbol.
🚀 Ejecución paso a paso
| Paso | Nodo emisor | Nodo receptor | Descripción |
|---|---|---|---|
| 1 | 0 | 1 | Nodo 0 envía a su hijo 1 |
| 2 | 0 | 2 | Nodo 0 envía a su hijo 2 |
| 3 | 0 | 3 | Nodo 0 envía a su hijo 3 |
| 4 | 2 | 4 | Nodo 2 reenvía a su hijo 4 |
| 5 | 3 | 5 | Nodo 3 reenvía a su hijo 5 |
| 6 | 5 | 6 | Nodo 5 reenvía a su hijo 6 |
✅ Resultado final
Todos los nodos reciben el mensaje, usando solo n - 1 = 6 mensajes.
| Nodo | ¿Recibió el mensaje? |
|---|---|
| 0 | Sí (es la raíz) |
| 1 | Sí |
| 2 | Sí |
| 3 | Sí |
| 4 | Sí |
| 5 | Sí |
| 6 | Sí |
💬 Observaciones
- Mensajes totales:
n - 1 = 6 - Es la forma más eficiente si ya tenemos el árbol.
- Permite paralelismo: varios nodos pueden reenviar a la vez.
- Ideal para redes distribuidas con vecindades limitadas (no totalmente conectadas).
- Si se necesita hacer una suma global, se puede hacer un recorrido postorden (bottom-up), y luego difundir el resultado (top-down).
2) Token passing con mensajes asincrónicos#
Implemente una solución al problema de exclusión mutua distribuida entre N procesos utilizado un algoritmo de tipo token passing con mensajes asincrónicos.
El algoritmo de token passing, se basa en un tipo especial de mensaje o “token” que puede utilizarse para otorgar un permiso (control) o para recoger información global de la arquitectura distribuida.
Si User[1:n] son un conjunto de procesos de aplicación que contienen secciones críticas y no críticas. Hay que desarrollar los protocolos de interacción (E/S a las secciones críticas), asegurando exclusión mútua, no deadlock, evitar demoras innecesarias y eventualmente fairness.
Para no ocupar los procesos User en el manejo de los tokens, ideamos un proceso auxiliar (helper) por cada User, de modo de manejar la circulación de los tokens. Cuando helper[i] tiene el token adecuado, significa que User[i] tendrá prioridad para acceder a la sección crítica.
chan canal_token[n]() ; # para envío de tokens
chan canal_solicitud_entrada[n]()
chan canal_permiso_entrada[n]()
chan canal_salida_seccion_critica[n](); # para comunicación proceso-helper
process ProcesoHelper[i = 1..N] {
while(true){
receive canal_token[i](); //Recibe el token desde el proceso anterior
if(!(empty(canal_solicitud_entrada[i]))){
receive canal_solicitud_entrada[i](); // Atiende la solicitud
send canal_permiso_entrada[i](); // Le da permiso para entrar a SC
receive canal_salida_seccion_critica[i](); // Espera a que salga
}
send canal_token[i MOD N + 1]();
}
}
process ProcesoUsuario[i = 1..N] {
while(true){
send canal_solicitud_entrada[i]();
receive canal_permiso_entrada[i]();
... sección crítica ...
send canal_salida_seccion_critica[i]();
... sección no crítica ...
}
}Se asume que el primero ya tenga el token
Suponga que N Procesos#
Suponga que N procesos poseen inicialmente cada uno un valor. Se debe calcular el promedio de todos los valores y al finalizar la computación todos deben conocer dicho promedio.
a) Describa conceptualmente las soluciones posibles con memoria distribuida para arquitecturas en estrella (centralizada), anillo circular, totalmente conectada y árbol.
Estrella (centralizada)
Cada proceso envía su valor al coordinador. Este los suma, divide por N para obtener el promedio y lo reenvía a todos.
Cantidad de mensajes: 2(N - 1), o N si hay broadcast.
Paralelismo solo en el envío inicial. El coordinador es cuello de botella y único punto de falla.
Anillo circular
Un proceso (ej. P0) inicia la suma parcial pasando su valor al siguiente. Cada proceso suma y reenvía. Al completar la vuelta, se divide entre N para obtener el promedio, que luego se difunde por el anillo.
Cantidad de mensajes: 2(N - 1).
No hay paralelismo: cada proceso espera al anterior.
Totalmente conectada
Cada proceso envía su valor a todos los demás. Luego calcula localmente el promedio.
Cantidad de mensajes: N(N - 1), o N si hay broadcast.
Alta velocidad gracias al paralelismo completo, pero alto costo en comunicación.
Árbol
Se construye un árbol donde cada nodo envía su valor a su padre (bottom-up) para sumar. La raíz calcula el promedio dividiendo la suma por N, y luego lo difunde (top-down).
Cantidad de mensajes: 2(N - 1).
Hay cierto grado de paralelismo en ambas etapas (varios hijos pueden enviar al mismo tiempo).
b) Implemente al menos 2 de las soluciones.
Estrella (centralizada)
chan canal_valores(INT);
chan canal_promedios[n](REAL promedio);
process Coordinador[0]{ // Coordinador
INT valor_local;
INT suma_total = valor_local;
REAL promedio_global;
for (i = 1 to n - 1) {
INT valor_recibido;
receive canal_valores(valor_recibido);
suma = suma + valor_recibido;
}
promedio_global = suma_total / n;
for (i = 1 to n - 1)
send canal_promedios[i](promedio_global);
}
process ProcesoTrabajador[i = 1 to n - 1]{ // Cada proceso envía su valor y recibe el promedio
INT valor_local;
REAL promedio_recibido;
send canal_valores(valor_local);
receive canal_promedios[i](promedio_recibido);
}Anillo circular
chan canal_suma[n](INT suma_parcial); // Para pasar sumas parciales en el anillo
chan canal_promedio[n](REAL promedio_global); // Para difundir el promedio calculado
process ProcesoInicial[0] {
INT valor_local
INT suma_total = valor_local;
REAL promedio_calculado;
// Fase 1
send canal_suma[1](suma_total);
//Fase 2
receive canal_suma[0](suma_total);
promedio_calculado = suma_total / n;
send canal_promedio[1](promedio_calculado);
}
process ProcesoAnillo[i = 1 to n - 1] {
INT valor_local,
INT suma_total;
REAL promedio_recibido;
INT siguiente = (i + 1) mod n; // El siguiente proceso en el anillo
// Fase 1: recibe suma parcial, acumula y reenvía
receive canal_suma[i](suma_total);
suma_total = suma_total + v;
send canal_suma[siguiente](suma_total);
// Fase 2: recibe el promedio y lo reenvía
receive canal_promedio[i](promedio_recibido);
if (i < n - 1)
send canal_promedio[siguiente](promedio_recibido);
}Totalmente conectada (simetrica)
chan canal_valores[n](INT valor_recibido); // Canal para intercambio de valores entre todos los procesos
process ProcesoSimetrico[i = 0 to n - 1] {
INT valor_local = ...;
INT suma_total = valor_local ;
REAL promedio_local;
// Envío mi valor_local a todos los demás procesos
for (int destino = 0 to n - 1 st destino <> i)
send canal_valores[k](valor_local );
// Recibo los valores de los demás procesos y acumulo la suma
for (int origen = 0 to n - 1 st origen <> i) {
INT valor_recibido
receive canal_valores[i](valor_recibido);
suma_total = suma_total + valor_recibido;
}
// Calculo el promedio de todos los valores
promedio_local = suma_total / n;
}c) Para cada una de las soluciones (todas), calcule la cantidad de mensajes y el tiempo (considerando que eventualmente hay operaciones que pueden realizarse concurrentemente).
Instancie c) para N=4, N=8, N=16, N=32 y N=64. Analice la performance para cada caso y compare las soluciones.
Nota: puede suponer que cada una de las operaciones tarda una unidad de tiempo.
Estrella (centralizada)
- Fórmula de mensajes:
2(n - 1)sin broadcast ,ncon broadcast - Fórmula de tiempo: Envío (1) + procesamiento (1) + difusión (1) = 3
Resultados:
- N = 4 → Mensajes:
2(4 - 1) = 6, Tiempo: 3 - N = 8 → Mensajes:
2(8 - 1) = 14, Tiempo: 3 - N = 16 → Mensajes:
2(16 - 1) = 30, Tiempo: 3 - N = 32 → Mensajes:
2(32 - 1) = 62, Tiempo: 3 - N = 64 → Mensajes:
2(64 - 1) = 126, Tiempo: 3
Anillo circular
- Fórmula de mensajes:
2(n - 1)(una vuelta para la suma + una vuelta para difusión) - Fórmula de tiempo:
2(n - 1)(no hay paralelismo)
Resultado
- N = 4 → Mensajes:
2(4 - 1) = 6, Tiempo: 6 - N = 8 → Mensajes:
2(8 - 1) = 14, Tiempo: 14 - N = 16 → Mensajes:
2(16 - 1) = 30, Tiempo: 30 - N = 32 → Mensajes:
2(32 - 1) = 62, Tiempo: 62 - N = 64 → Mensajes:
2(64 - 1) = 126, Tiempo: 126
Totalmente conectada
- Fórmula de mensajes:
n(n - 1)sin broadcastncon broadcast - Fórmula de tiempo: Envío + recepción, ambos en paralelo = 2
Resultados:
- N = 4 → Mensajes:
4 × (4 - 1) = 12, Tiempo: 2 - N = 8 → Mensajes:
8 × (8 - 1) = 56, Tiempo: 2 - N = 16 → Mensajes:
16 × (16 - 1) = 240, Tiempo: 2 - N = 32 → Mensajes:
32 × (32 - 1) = 992, Tiempo: 2 - N = 64 → Mensajes:
64 × (64 - 1) = 4032, Tiempo: 2
Árbol
- Fórmula de mensajes:
2(n - 1)(una subida bottom-up + una bajada top-down) - Fórmula de tiempo:
2 × log₂(n)(dos recorridos del árbol)
Resultados: (Suavemente redondeado para log₂(n))
- N = 4 → Mensajes:
2(4 - 1) = 6, Tiempo:2 × 2 = 4 - N = 8 → Mensajes:
2(8 - 1) = 14, Tiempo:2 × 3 = 6 - N = 16 → Mensajes:
2(16 - 1) = 30, Tiempo:2 × 4 = 8 - N = 32 → Mensajes:
2(32 - 1) = 62, Tiempo:2 × 5 = 10 - N = 64 → Mensajes:
2(64 - 1) = 126, Tiempo:2 × 6 = 12
Suponga una ciudad representada por una matriz#
Exclusión mutua distribuida#
Implemente una solución al problema de exclusión mutua distribuida entre N procesos utilizando un algoritmo Token Passing con PMA.
Una ciudad representada por una matriz#
Suponga una ciudad representada por una matriz A(n×n). De cada esquina x, y se conocen dos valores enteros que representan la cantidad de autos y motos que cruzaron en la última hora. Los valores de cada esquina son mantenidos por un proceso distinto P(x, y). Cada proceso puede comunicarse con sus vecinos izquierdo, derecho, arriba y abajo, y también con los de las 4 diagonales (los procesos de las esquinas tienen sólo 3 vecinos y los otros en los bordes de la grilla tienen 5 vecinos).
a) Escriba un algoritmo Heartbeat que calcule las esquinas donde cruzaron la mayor cantidad de autos y la menor cantidad de motos respectivamente, de forma que al terminar el programa, cada proceso conozca ambos valores.
Nota: Indicar qué tipo de pasajes de mensajes se va a utilizar. Justificar la elección.
b) Analizar desde el punto de vista de la cantidad de mensajes.
c) Analizar cómo podría mejorarse la cantidad de mensajes.
d) Analizar qué pasaría si no existieran las diagonales.
Exclusión mutua distribuida#
Implemente una solución al problema de exclusión mutua distribuida entre N procesos utilizando un algoritmo token passing con mensajes asincrónicos.
Solución al problema del pruducto de matrices#
Sea la siguiente solución al problema del producto de matrices de n×n con P procesos en paralelo con variables compartidas.
process worker [w = 1 to P] { # strips en paralelo (p strips de n/P filas)
int first = (w - 1) * n / P + 1; # Primera fila del strip
int last = first + n/P - 1; # Última fila del strip
for (i = first to last) {
for (j = 1 to n) {
c[i,j] = 0.0;
for (k = 1 to n)
c[i,j] = c[i,j] + a[i,k] * b[k,j];
}
}
}Suponga n = 512 y cada procesador capaz de ejecutar un proceso.
a) Calcular cuántas asignaciones, sumas y productos se hacen secuencialmente (caso en que P=1), y cuántas se realizan en cada procesador en la solución paralela con P=8.
b) Si los procesadores P1 a P7 son idénticos, con tiempos de asignación 1, de suma 2 y de producto 3, y si el procesador P8 es 3 veces más lento, calcule cuánto tarda el proceso total concurrente.
c) ¿Cuál es el valor del speedup?
d) ¿Cómo modificaría el código para lograr un mejor speedup?
NOTA: para realizar los cálculos no tenga en cuenta las operaciones de asignación e incremento correspondientes a las sentencias for.
Defina los paradigmas de interacción#
Defina los paradigmas de interacción entre procesos distribuidos heartbeat, servidores replicados y token passing.
Marque ventajas y desventajas en cada uno de ellos cuando se utiliza comunicación por mensajes sincrónicos o asincrónicos.
Suponga que N Procesos#
Suponga que N procesos poseen inicialmente cada uno un valor. Se debe calcular el promedio de todos los valores y al finalizar la computación todos deben conocer dicho promedio.
a) Describa conceptualmente las soluciones posibles con memoria distribuida para arquitecturas en estrella (centralizada), anillo circular, totalmente conectada y árbol.
b) Implemente al menos 2 de las soluciones.
c) Para cada una de las soluciones (todas), calcule la cantidad de mensajes y el tiempo (considerando que eventualmente hay operaciones que pueden realizarse concurrentemente).
Instancie c) para N = 4, N = 8, N = 16, N = 32 y N = 64. Analice la performance para cada caso y compare las soluciones.
Nota: puede suponer que cada una de las operaciones tarda una unidad de tiempo.
Suponga que N Procesos#
Suponga que N procesos poseen inicialmente cada uno un valor.
Se debe calcular el promedio de todos los valores y al finalizar la computación todos deben conocer dicho promedio.
a. Describa conceptualmente las soluciones posibles con memoria distribuida para arquitectura en
estrella (centralizada), anillo circular, totalmente conectada y árbol.
b. Implemente al menos 2 de las soluciones.
c. Para cada una de las soluciones (todas), calcule la cantidad de mensajes y el tiempo.
Instancie c) para N = 4, N = 8, N = 16, N = 32 y N = 64.
Analice la performance en cada caso y compare las soluciones.
NOTA: Puede suponer que cada una de las operaciones tarda una unidad de tiempo.
Suponga que N Procesos#
Suponga que N procesos poseen inicialmente cada uno un valor. Se debe calcular la suma de todos los valores y al finalizar la computación todos deben conocer dicha suma.
Analice (desde el punto de vista del número de mensajes y la performance global) las soluciones posibles con memoria distribuida para arquitecturas en Estrella (centralizada), Anillo Circular, Totalmente Conectada y Árbol.
Definir conceptualmente y decir cantidad de mensajes de cada uno. Implementar dos de esos.
En la mesa de mayo eran los mismos ejercicios excepto el último: había que implementar heartbeat o passing the baton (se elegía uno de los dos).
Suponga que N Procesos#
Implemente una solución al problema de exclusión mutua distribuida entre n procesos utilizando un algoritmo Token Passing con mensajes asincrónicos.
Suponga una ciudad representada por una matriz#
Suponga una ciudad representada por una matriz A(n×n). De cada esquina x, y se conocen dos valores enteros que representan la cantidad de autos y motos que cruzaron en la última hora. Los valores de cada esquina son mantenidos por un proceso distinto P(x,y).
Cada proceso puede comunicarse con sus vecinos izquierdo, derecho, arriba y abajo, y también con los de las 4 diagonales (los procesos de las esquinas tienen solo 3 vecinos y los otros en los bordes de la grilla tienen 5 vecinos).
Suponga que N Procesos#
Suponga que N procesos poseen inicialmente cada uno un valor.
Se debe calcular el promedio de todos los valores y al finalizar la computación todos deben conocer dicho promedio.
a. Describa conceptualmente las soluciones posibles con memoria distribuida para arquitectura en estrella (centralizada), anillo circular, totalmente conectada y árbol.
b. Implemente al menos 2 de las soluciones.
c. Para cada una de las soluciones (todas), calcule la cantidad de mensajes y el tiempo.
Instancie c) para N = 4, N = 8, N = 16, N = 32 y N = 64.
Analice la performance en cada caso y compare las soluciones.
NOTA: Puede suponer que cada una de las operaciones tarda una unidad de tiempo.
📌 Preguntas Practicas FIJAS#

1) Calculos con Matrices#
Sea la siguiente solución al problema del producto de matrices de nxn con P procesos trabajando en paralelo.
process worker[w = 1 to P] { // strips en paralelo (P strips de n/P filas)
int first = (w - 1) * n / P; // Primera fila del strip
int last = first + n / P - 1; // Última fila del strip
for (i = first to last) {
for (j = 0 to n - 1) {
c[i,j] = 0.0;
for (k = 0 to n - 1)
c[i,j] = c[i,j] + a[i,k] * b[k,j];
}
}
}a) Suponga que n = 128 y cada procesador es capaz de ejecutar un proceso. ¿Cuántas asignaciones, sumas y productos se hacen secuencialmente (caso en que P = 1)?
- Asignaciones
128^3+128^2->2.097.152+16.384->2.113.536 - Sumas
128^3->2.097.152 - Productos
128^3->2.097.152
b) ¿Cuántas se realizan en cada procesador en la solución paralela con P = 8?
- Strip 128/8 = 16 Filas por procesador (MIRA EL CODIGO O PEGO 👊)
- Asignaciones
16 * 128^2+16 * 128->262.144+2048->264.192 - Sumas
16 * 128^2->262.144 - Productos
16 * 128^2->262.144
c) Si los procesadores P1 a P7 son iguales, y sus tiempos de asignación son 1, de suma 2 y de producto 3, y si P8 es 4 veces más lento,
¿Cuánto tarda el proceso total concurrente?
T(P1-P7)-> (264.192 * 1) + (262.144 * 2) + (262.144 * 3) -> 264.192 + 524.288 + 786.432 ->1.574.912T(P8)->T(P1-P7) * 4->1.574.912 * 4->6.299.648(El tiempo paralelo)
¿Cuál es el valor del speedup (Tiempo secuencial / Tiempo paralelo)?
Tiempo Total Secuencial= (2.113.536 * 1) + 2.097.152 * 2) + 2.097.152 * 3) ->12.599.296Speedup=T(secuencial) / T(paralelo)->(12.599.296) / (6.299.648)->2.02
Modifique el código para lograr un mejor speedup. (Este punto no se como hacerlo) (Le tenemos que dejar la menor cantidad de filas posibles a P8 ya que tarda un 🥚)
- Multiplo(7) mas cercano a 128 -> 126
- Strip P8 -> 2 filas (128 - 126)
- Strip P1-P7 -> 18 filas (126/7)
Calculamos los tiempos para P8 con la nueva distribución de filas:
- Asignaciones
2 * 128^2+2 * 128->32.768+256->33.024 - Sumas
2 * 128^2->32.768 - Productos
2 * 128^2->32.768 T(P8)-> (33.024 * 1) + (32.768 * 2) + (32.768 * 3) -> 33.024 + 65.536 + 98.304 ->196.864- T(P8) -> TP8 * 4 ->
196.864 * 4->787.456
Calculamos el tiempo para P1-P7:
- Asignaciones
18 * 128^2+18 * 128->294.912+2.304->297.216 - Sumas
18 * 128^2->294.912 - Productos
18 * 128^2->294.912 T(P1-P7)-> (297.216 * 1) + (294.912 * 2) + (294.912 * 3) -> 297.216 + 589.824 + 884.736 ->1.771.776
Como el tiempo mas grande es el de T(P1-P7) el tiempo paralelo es: 1.771.776 y volvemos a calcular el speedup:
Speedup=T(secuencial) / T(paralelo)->(12.599.296) / (1.771.776)->7.11
2) Cuales Cumplen con ASV#
Dado el siguiente programa concurrente con memoria compartida:
|
|
Una asignación
|
Referencia critica se da cuanto estas leyendo una variable que es modificada por otro proceso concurrente
a) ¿Cuáles de las asignaciones dentro de la sentencia co cumplen la propiedad de ASV? Justifique claramente.
| Instrucción | ¿Cumple_ASV? | Justificación |
|---|---|---|
| X := X - Z | ✅ Sí | ”e” tiene a lo sumo una referencia critica (X - Z), y la variable x no es referenciada en otros procesos (X) |
| Z := Z * 2 | ✅ Sí | ”e” no contiene niguna referencia critica (Z * 4), en cullo caso x puede ser leida por otros procesos (Z) |
| Y := Z + 4 | ✅ Sí | ”e” tiene a lo sumo 1 referencia critica (Z + 4), y la variable x no es referenciada por otros procesos (Y) |
b) Indique los resultados posibles de la ejecución. Justifique.
Cada tarea se ejecuta sin ninguna interrupción hasta que termina (Si una sentencia no es atómica se puede cortar su ejecución pero al cumplir ASV la ejecución no se ve afectada) y las llamamos T1, T2 y T3 respectivamente obtenemos el siguiente subconjunto de historias:
- T1, T2, T3 => X=1, Z=6, y=10
- T1, T3, T2 => X=1, Z=6, y=7
- T2, T1, T3 => X=-2, Z=6, y=10
- T2, T3, T1 => X=-2, Z=6, y=10
- T3, T1, T2 => X=1, Z=6, y=7
- T3, T2, T1 => X=-2, Z=6, y=7
Explicación:
- El valor de Z es siempre el mismo ya que no posee ninguna referencia crítica.
- Los valores de X e Y se ven afectados por la ejecución de T2 ya que sus resultados dependen de la referencia que hacen a la variable Z que es modificada.
- Entonces, si T1 y T3 se ejecutan antes que T2 ambas usarán el valor inicial de Z que es 3 obteniendo los resultados X=1 e Y=7;
- Ahora si T2 se ejecuta antes que las demás los resultados serán X=-2 e Y=10 y por último, tenemos los casos en que T2 se ejecuta en medio con T1 antes y T3 después o con T3 antes y T1 después.
3) Cuales Cumplen con ASV 2#
Dado el siguiente programa concurrente con memoria compartida:
x = 3; y = 2; z = 5;
co
x = y * z
z = z * 2
y = y + 2x
oca) ¿Cuáles de las asignaciones dentro de la sentencia co cumplen la propiedad de “A lo sumo una vez”? Justifique claramente.
| Instrucción | ¿Cumple_ASV? | Justificación |
|---|---|---|
| X = Y * Z | ❌ No | ”e” tiene dos referencias criticas (X - Z) |
| Z = Z * 2 | ✅ Sí | ”e” no contiene niguna referencia critica (Z * 2), en cullo caso x puede ser leida por otros procesos (Z) |
| Y = Y + 2X | ❌ No | ”e” tiene a lo sumo 1 referencia critica (Y + 2X), y la variable x es referenciada por otros procesos (Y) |
b) Indique los resultados posibles de la ejecución. Justifique.
- A, B y C o A, C y B -> x = 10; z = 10; y = 22
- C, B y A o B, C y A -> x = 80; z = 10; y = 8
- C, A y B -> x = 40; z = 10; y = 8
- B, A y C-> x = 20; z = 10; y = 42
Si se empieza a ejecutar A leyendo a y = 2, y en ese momento se ejecuta C leyendo a x = 3 (porque no terminó la asignación de A), y luego termina lo que falta de A y se ejecuta B:
- x = 10; z = 10; y = 8
Si se empieza a ejecutar A leyendo a y = 2, y en ese momento se ejecuta C leyendo a x = 3 (porque no terminó la asignación de A), y luego se ejecuta B y lo que falta de A:
- x = 20; z = 10; y = 8
4) Numero de Mensajes y Granularidad#
Suponga los siguientes programas concurrentes. Asuma que “función” existe, y que los procesos son iniciados desde el programa principal.
| P1 | P2 |
|
|
a) Analice desde el punto de vista del número de mensajes.
En P1 se envían solo 10 mensajes (uno por cada bloque de 10000), mientras que en P2 se envían 10000 mensajes (uno por cada bloque de 10), por lo que P1 es mucho más eficiente en términos de comunicación.
b) Analice desde el punto de vista de la granularidad de los procesos.
En P1, la comunicación es poco frecuente y el cómputo por mensaje es alto, por lo que tiene granularidad gruesa.
En P2, hay mucha más comunicación en menos tiempo, lo que implica granularidad fina, mayor concurrencia pero también más sobrecarga.
Prioridad y Granularidad
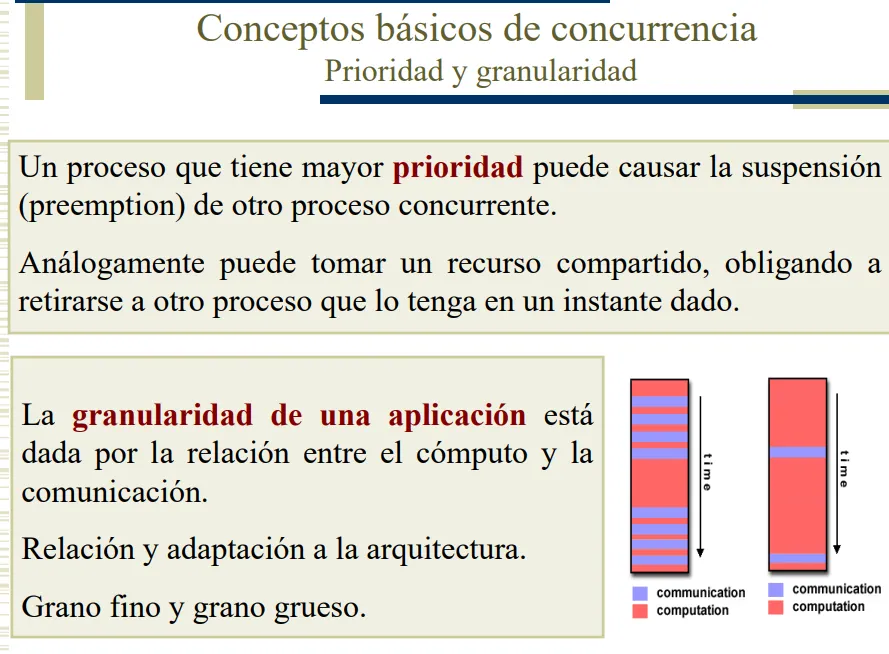
c) Cuál de los programas le parece más adecuado para ejecutar sobre una arquitectura de tipo cluster de PCs? Justifique.
La implementación más adecuada para este tipo de arquitecturas es P1, por ser de granularidad gruesa. Al tratarse de una arquitectura con memoria distribuida la comunicación entre los procesos es más costosa ya que cada proceso puede ejecutarse en computadores diferentes, por lo tanto sería más eficiente que la sobrecarga de comunicación sea lo más baja posible, y dicha característica la brinda la granularidad gruesa.
5) Numero de Mensajes y Granularidad 2#
Suponga los siguientes programas concurrentes. Asuma que EOS es un valor especial que indica el fin de la secuencia de mensajes, y que los procesos son iniciados desde el programa principal.
| P1 | P2 |
|
|
a) ¿Qué hacen los programas?
Ambos suman todos los elementos de una matriz 10000×10000, pero:
- P1:
Generaenvía cada elemento (100M mensajes) yAcumulasuma todo. - P2:
Generasuma por fila y envía 1 valor por fila (10K mensajes);Acumulasuma esos totales.
Conclusión: Hacen lo mismo, pero P2 es mucho más eficiente en comunicación y procesamiento.
b) Analice desde el punto de vista del número de mensajes.
Desde el punto de vista de los mensajes, P1 envía 100 millones y P2 solo 10000, por lo que P2 es mucho más eficiente en comunicación.
c) Analice desde el punto de vista de la granularidad de los procesos.
Desde el punto de vista de granularidad, P2 tiene un grano más grueso que P1 porque realiza más cómputo local y menos comunicación, lo que mejora la eficiencia.
🧩 ¿Qué es la granularidad?
La granularidad de una aplicación concurrente o paralela se refiere a la relación entre el tiempo dedicado al cómputo y el tiempo dedicado a la comunicación entre procesos o hilos.
- Si una aplicación realiza mucho cómputo local antes de necesitar comunicarse, se dice que tiene grano grueso.
- Si, por el contrario, realiza frecuentes comunicaciones con poco cómputo entre medio, se dice que tiene grano fino.
Esta característica es clave para el diseño y rendimiento de programas paralelos, ya que:
- Grano grueso suele ser más eficiente en arquitecturas donde la comunicación es costosa.
- Grano fino puede aprovechar mejor arquitecturas con alta velocidad de comunicación o memoria compartida eficiente.
🔧 Resumen:
La granularidad es la proporción entre el cómputo y la comunicación en una aplicación. Afecta cómo se adapta el programa a una arquitectura paralela, diferenciándose entre grano fino (más comunicación) y grano grueso (más procesamiento local).
d) ¿Cuál de los programas le parece más adecuado para ejecutar sobre una arquitectura de tipo cluster de PCs? Justifique.
P2, porque en clusters la comunicación es costosa y se prioriza el cómputo local.
P2 reduce drásticamente los mensajes (de 100M a 10K), adaptándose mejor al grano grueso que requieren estas arquitecturas.
6) Indicar para cada Item si son Equivalentes#
Dados los siguientes dos segmentos de codigo, indicar para cada uno de los ítems si son equivalentes o no. Justificar cada caso (de ser necesario dar ejemplos).
|
|
Dado que ambos comienzan con cant = 1000, se ejecuta la rama (cant > 10). La diferencia clave está en el comportamiento ante guardas no habilitadas
- En el Segmento 1 (DO), si ninguna guarda es verdadera, el ciclo termina.
- En el Segmento 2 (while true), si ninguna guarda es verdadera, el programa se bloquea.
Para que sean equivalentes, debe haber una guarda siempre habilitada, como INCOGNITA.
- a) INCOGNITA equivale a: (cant = 0) No son equivalentes si INCOGNITA solo cubre cant == 0, ya que valores como cant = 5 no están contemplados.
- b) INCOGNITA equivale a: (cant > -100) Ambos segmentos son equivalentes si INCOGNITA ≡ (cant > -100), ya que siempre hay una guarda habilitada y el ciclo no se detiene.
- c) INCOGNITA equivale a: ((cant > 0) or (cant < 0)) Ambos segmentos no son equivalentes porque con
cant = 0ninguna guarda se cumple: elDOfinaliza, pero elwhile (true)queda bloqueado. - d) INCOGNITA equivale a: ((cant > -10) or (cant < 10)) Los segmentos no son equivalentes porque con
cant = 10o-10ninguna guarda se cumple: elDOfinaliza, pero elwhile (true)queda bloqueado. - e) INCOGNITA equivale a: ((cant >= -10) or (cant <= 10)) Con esta condición, los segmentos son equivalentes porque la guarda cubre todos los casos y garantiza que siempre haya al menos una rama habilitada.
7) ¿Que valores quedan?#
4. Dado el siguiente bloque de código, indique para cada inciso qué valor queda en aux, o si el código queda bloqueado. Justifique sus respuestas.
aux := -1;
...
if (A == 0); P2?(aux) → aux = aux + 2;
▭ (A == 1); P3?(aux) → aux = aux + 5;
▭ (B == 0); P3?(aux) → aux = aux + 7;
end if;i. Si el valor de A = 1 y B = 2 antes del if, y solo P2 envia el valor 6. >> Solo se habilita la rama (A == 1); P3?(aux), pero como P3 no envía ningún valor, el código queda bloqueado esperando recibir de P3.
ii. Si el valor de A = 0 y B = 2 antes del if, y solo P2 envia el valor 8. >> Se habilita la guarda (A == 0); P2?(aux) y como P2 envía 8, se recibe y se ejecuta aux = 8 + 2, resultando en aux = 10.
iii. Si el valor de A = 2 y B = 0 antes del if, y solo P3 envia el valor 6. >> iii. Se habilita la guarda (B == 0); P3?(aux) y como P3 envía 6, se recibe y se ejecuta aux = 6 + 7, dando como resultado aux = 13.
iv. Si el valor de A = 2 y B = 1 antes del if, y solo P3 envia el valor 9 >> Todas las guardas son falsas, por lo que el if no se ejecuta, el código no se bloquea y aux permanece en -1.
v. Si el valor de A = 1 y B = 0 antes del if, y solo P3 envia el valor 14 >> Las guardas (A == 1) y (B == 0) son verdaderas, ambas con P3?(aux), por lo que al recibir 14 se elige una de forma no determinista y aux será 19 (14+5) o 21 (14+7).
vi. Si el valor de A = 0 y B = 0 antes del if, P3 envia el valor 9 y P2 el valor 5. >> Las guardas (A == 0) y (B == 0) son verdaderas; como P2 envía 5 y P3 envía 9, se elige una rama al azar y aux será 7 (5+2) o 16 (9+7).
8) ¿Que valores quedan? 2#
Dado el siguiente programa concurrente con memoria compartida, y suponiendo que todas las variables están inicializadas en 0 al empezar el programa y las instrucciones NO son atómicas. Para cada una de las opciones indique verdadero o falso.
En caso de ser verdadero indique el camino de ejecución para llegar a ese valor, y en caso de ser falso justifique claramente su respuesta.
| P1 | P2 | P3 |
|
|
|
a) El valor de x al terminar el programa es 9.
🔎 Probamos combinaciones buscando x = 9
❌ Caso 1: P1 completo → P2 → P3
// P1 ejecuta completo:
x = 0 → entra al if
y = 4*0 + 2 = 2
x = y + 2 + x = 2 + 2 + 0 = 4
// P2 ejecuta:
x = 4 + 1 = 5
// P3 ejecuta:
x = 10 * 5 + 1 = 51 → ❌ no es 9❌ Caso 2: P2 → P3
// P2 ejecuta:
x = 0 + 1 = 1
// P3 ejecuta:
x = 10 * 1 + 1 = 11 → ❌❌ Caso 3: P3 → P2
// P3 ejecuta:
x = 10 * 0 + 1 = 1
// P2 ejecuta:
x = 1 + 1 = 2 → ❌❌ Caso 4: P3 con x = 2
// Supongamos que x llega a 2 por P2 → P2
x = 0 + 1 = 1
x = 1 + 1 = 2
// P3 ejecuta:
x = 10 * 2 + 1 = 21 → ❌❌ Conclusión del inciso a)
✅ x = 9 no se puede alcanzar, porque:
- P1 produce como mucho x = 4
- P2 suma 1 cada vez
- P3 hace
x = 10 * x + 1, lo cual siempre da un número impar mayor (nunca 9)
✅ Respuesta final del inciso a):
FALSO – No existe ninguna secuencia de ejecución posible que lleve a x = 9.
b) El valor de x al terminar el programa es 6.
✔️ Verdadero
Una posible traza:
- P1 ejecuta parcialmente:
y := 4 * 0 + 2 = 2 - P3 ejecuta:
x := 0 * 8 + 0 * 2 + 1 = 1 - P2 ejecuta:
x := 1 + 1 = 2 - P1 finaliza:
x := y + 2 + x = 2 + 2 + 2 = 6
Por lo tanto, es posible llegar a
x = 6.
c) El valor de x al terminar el programa es 11.
✔️ Verdadero
Una traza simple:
- P2 ejecuta:
x := 1 - P3 ejecuta:
x := 10 * 1 + 1 = 11
P1 no entra porque
x ≠ 0.
Resultado final:x = 11→ válido.
d) Y siempre termina con alguno de los siguientes valores: 10, 6, 2, 0.
✔️ Verdadero
Análisis por casos:
y = 0: si P1 no ejecuta el cuerpo delif(porquex ≠ 0al momento de evaluarlo)y = 2: si P1 ejecuta elifconx = 0, y aún no ha sido modificadoy = 6: six = 1al momento de ejecutary := 4 * x + 2y = 10: six = 2cuando se evalúa la asignación
Como la asignación de
ydepende directamente del valor dex, que puede ser modificado por otros procesos antes de ejecutarla, solo esos cuatro valores son posibles.
9) La solución a un problema es paralelizada#
Suponga que la solución a un problema es paralelizada sobre p procesadores de dos maneras diferentes.
- En un caso, el speedup (S) está regido por la función S=p-1 y
- en el otro por la función S=p/2.
¿Cuál de las dos soluciones se comportará más eficientemente al crecer la cantidad de procesadores? Justifique claramente.
De las dos soluciones, la que tiene speedup S = p - 1 se comporta de forma más eficiente a medida que crece el número de procesadores.
Esto se debe a que el speedup ideal es S = p, y:
S = p - 1 crece casi linealmente y se acerca al ideal.
S = p / 2 crece más lentamente y siempre es la mitad del número de procesadores.
Si analizamos la eficiencia, que se define como:
E = S / p
- E = (p - 1) / p -> Esta eficiencia tiende a 1 cuando p crece.
- E = (p / 2) / p -> (p/2) / (p/1) -> (p * 1)/(2 * p) -> p/2p -> 1/2 -> La eficiencia es constante e igual al 50%, sin importar cuántos procesadores haya.
Por lo tanto, la solución con S = p - 1 es más eficiente, ya que utiliza mejor los procesadores disponibles.
Ahora suponga S = 1/p y S = 1/p^2
- Ambos speedups disminuyen con más procesadores (son inversamente proporcionales).
- Pero S = 1/p siempre es mayor que S = 1/(p^2).
- Lo mismo ocurre con la eficiencia: 1/(p^2) decrece más lento que 1/(p^3).
- Por eso, la solución con S = 1/p es más eficiente y escala mejor.
10) La solución a un problema es paralelizada 2#
Suponga que la solución a un problema es paralelizada sobre p procesadores de dos maneras diferentes.
- En un caso, el speedup (S) está regido por la función S=p/3
- y en el otro por la función S=p-3.
¿Cuál de las dos soluciones se comportará más eficientemente al crecer la cantidad de procesadores? Justifique claramente.
Suponiendo el uso de 5 procesadores:
- Opción 1: S = 5 / 3 ≈ 1.66
- Opción 2: S = 5 − 3 = 2
En este caso, la segunda opción es más eficiente porque alcanza un mayor speedup.
Ahora, incrementamos la cantidad de procesadores suponemos 100 procesadores:
- Solución 1 => S=100/3=33,33
- Solución 2 => S=100-3=97
Podemos decir, que a medida que p tiende a infinito, para la solución 1 siempre el Speedup será la tercera parte en cambio para la solución 2 el valor “-3” se vuelve despreciable.
Por lo tanto la solución 2 es la que se comporta más eficientemente al crecer la cantidad de procesadores.
11) La solución a un problema es paralelizada 3#
Suponga que la solución a un problema es paralelizada sobre p procesadores de dos maneras diferentes.
- En un caso, el speedup(s) esta regido por la función S = p-4
- y el otro por la función S = p/3 para p > 4.
¿Cuál de las dos soluciones se comportara más eficientemente al crecer la cantidad de procesadores?
- A medida que
pcrece, la eficiencia de S = p − 4 se acerca a 1 (ideal). - La eficiencia de S = p / 3 es constante y baja (0.33), sin importar el valor de
p. - Por eso, la función S = p − 4 se comporta mucho mejor para valores grandes de
p.
12) La solución a un problema es paralelizada 4#
Suponga que la solución a un problema es paralelizada sobre p procesadores de dos maneras diferentes.
- En un caso, la eficiencia está regido por la función E = 1/p
- y en el otro por la función E = 1/p^2.
¿Cuál de las dos soluciones se comportará más eficientemente al crecer la cantidad de procesadores? Justifique.
Respuesta
Claramente, a partir de p = 2, se observa que la eficiencia E₁ = 1/p es mayor que la eficiencia E₂ = 1/p². Analicemos algunos valores:
- Para p = 1:
E₁ = 1/1 = 1 E₂ = 1/1 = 1 - Para p = 2:
E₁ = 1/2 = 0.5 E₂ = 1/4 = 0.25 - Para p = 3:
E₁ = 1/3 ≈ 0.33 E₂ = 1/9 ≈ 0.11
Como se puede apreciar, E₁ siempre es mayor que E₂ a partir de p = 2, y ambas eficiencias decrecen al aumentar el número de procesadores.
Conclusión:
La solución con E = 1/p se comporta más eficientemente que la de E = 1/p², ya que decrece más lentamente. Sin embargo, ninguna de las dos escala bien cuando p crece mucho, ya que ambas tienden a eficiencia cero.
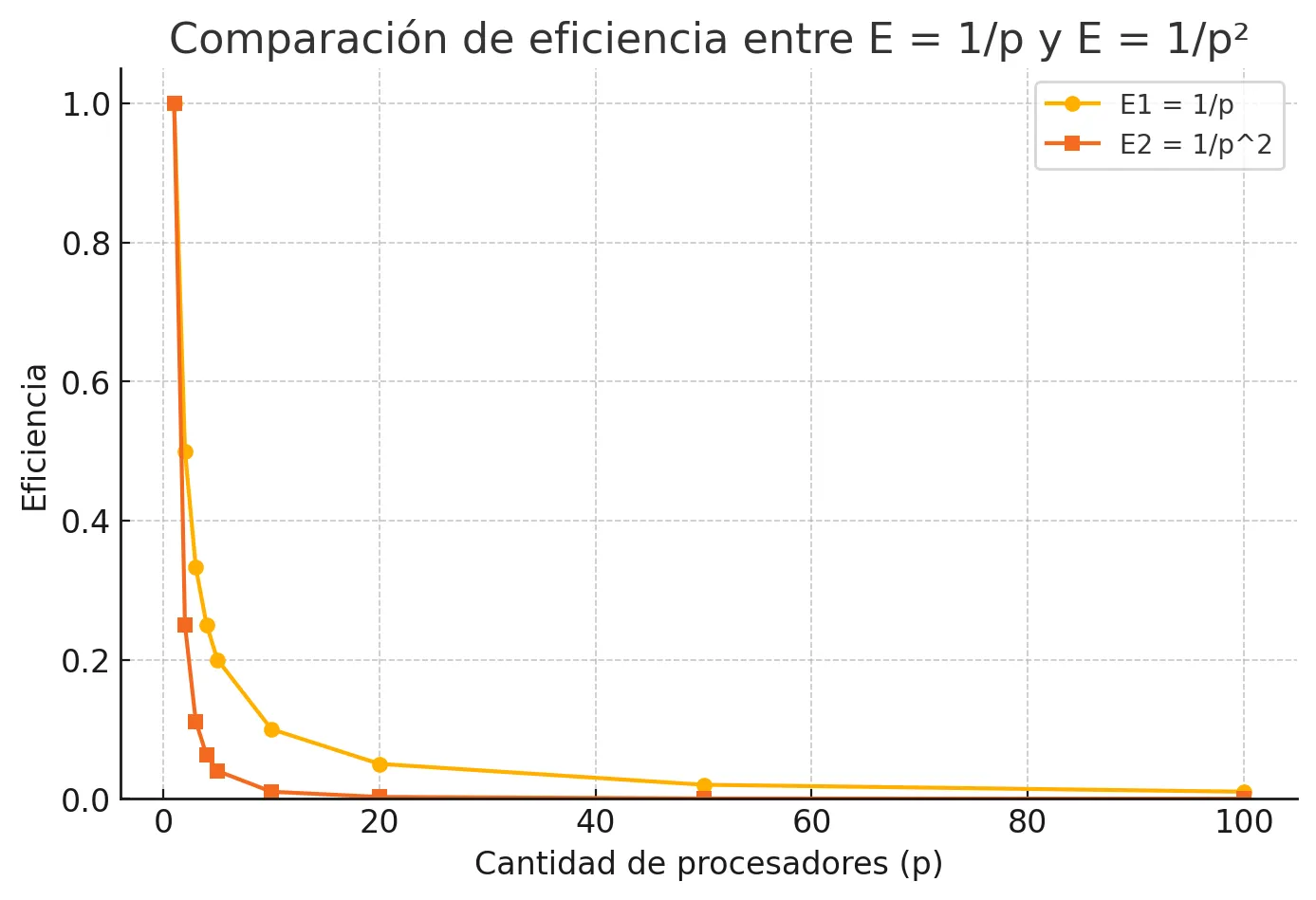
| Procesadores (p) | E1 = 1/p | E2 = 1/p² |
|---|---|---|
| 1 | 1.0000 | 1.0000 |
| 2 | 0.5000 | 0.2500 |
| 3 | 0.3333 | 0.1111 |
| 4 | 0.2500 | 0.0625 |
| 5 | 0.2000 | 0.0400 |
| 10 | 0.1000 | 0.0100 |
| 20 | 0.0500 | 0.0025 |
| 50 | 0.0200 | 0.0004 |
| 100 | 0.0100 | 0.0001 |
13) Suponga que el tiempo de ejecución de un algoritmo Secuencial#
Suponga que el tiempo de ejecución de un algoritmo secuencial es de 1000 unidades de tiempo, de las cuales el 80% corresponden a código paralelizable.
¿Cuál es el límite en la mejora que puede obtenerse paralelizando el algoritmo?
Tenemos un programa que tarda 1000 unidades de tiempo si lo ejecutamos de forma secuencial (1 solo procesador), pero el 80% de ese tiempo es paralelizable.
- 80% de 1000 = 800 unidades de tiempo paralelizable
- 20% de 1000 = 200 unidades de tiempo secuencial
Ley de Andahl
T_Paralelo = Porcion_T_secuencial + (Porcion_T_paralelizable / p)
Si usamos 800 procesadores, el tiempo de ejecución de la parte paralelizable se reduce a 1 unidad de tiempo.
- T_Paralelo = 200 + (800 / 800) -> 200 + 1 -> 201
- Speedup = T_secuencial / T_paralelo -> 1000 / 201 ≈ 4.975
Conviene usar una cantidad mas chica de procesadores que pueden estar trabajando todo el tiempo
- T_Paralelo = 200 + (800 / 5) = 200 + 160 = 360
- Speedup = 1000 / 360 ≈ 2.778
14) Suponga que el tiempo de ejecución de un algoritmo Secuencial 2#
Suponga que el tiempo de ejecución de un algoritmo secuencial es de 8000 unidades de tiempo, de las cuales solo el 90% corresponde a código paralelizable.
¿Cuál es el límite en la mejora que puede obtenerse paralelizando el algoritmo? Justifique.
T_Total = 8000 el 90% es paralelizable es decir 7200 y el 10% es secuencial es decir 800.
El mejor caso se da si usamos tantos procesadores como para la parte paralela tarde solo 1 unidad de tiempo (Es decir, 7200 procesadores para 7200 unidades paralelas).
T_Paralelo -> T_secuencial + T_paralelizable / p
- T_Paralelo -> 800 + 7200 / 7200 -> 800 + 1 -> 801
- Speedup = T_secuencial / T_Paralelo -> 8000 / 801 ≈ 9.99
El limite teorico de memoria es aproximadamente 10 veces mas rapido.
15) Suponga que el tiempo de ejecución de un algoritmo Secuencial 3#
Suponga que el tiempo de ejecución de un algoritmo secuencial es de 10000 unidades de tiempo, de las cuales 95% corresponden a código paralelizable.
¿Cuál es el límite en la mejora que puede obtenerse paralelinzado el algoritmo?
El limite se alncaza cuando se utilizan 9500 procesadores (uno por cada unidad de tiempo paralelizable), lo que reduce el tiempo de ejecución de la parte paralela a 1 unidad de tiempo.
La parte secuencial, que no puede paralelizarse, tarda 500 unidades de tiempo.
T_Paralelo = T_secuencial + T_paralelizable / p
- T_Paralelo = 500 + 9500 / 9500 -> 500 + 1 = 501
- Speedup = T_secuencial_total / T_Paralelo = 10000 / 501 ≈ 19.96
Este resultado confirma la Ley de Amdahl, la cual establece que el límite de paralelización de un algoritmo no depende de cuántos procesadores se usen, sino de cuánta parte del código es secuencial.
📢 Miralas de Reojo#

1) Propuesta al problema de alocación SJN#
Sea la siguiente solución propuesta al problema de alocación SJN (Short Job Next):
Monitor SJN {
Bool libre = true;
Cond turno;
Procedure request {
If (not libre) wait (turno, tiempo);
Libre = false;
}
Procedure release {
Libre = true;
Signal (turno);
}
}a) ¿Funciona correctamente con disciplina de señalización Signal and continue? Justifique.
👀 Respuesta
No, la solución no funciona correctamente con la disciplina de señalización Signal and Continue (S&C).
Bajo esta disciplina, cuando un proceso realiza un signal, continúa ejecutando dentro del monitor, y el proceso que fue despertado es enviado a la cola de listos (ready queue) del sistema operativo. Esto implica que su reingreso al monitor depende de la política de planificación del sistema, y no se garantiza que sea el próximo en ejecutarse.
En consecuencia, un proceso con menor tiempo (según la política Shortest Job Next) podría quedar retrasado si otro proceso ingresa antes al monitor. Por lo tanto, el orden de ejecución no refleja necesariamente la prioridad establecida por el parámetro tiempo, y no se cumple el objetivo del SJN.
Respuesta de un random
Con S&C un proceso que es despertado para poder seguir ejecutando es pasado a la cola de ready en cuyo caso su orden de ejecución depende de la política que se utilice para ordenar los procesos en dicha cola. Puede ser que sea retrasado en esa cola permitiendo que otro proceso ejecute en el monitor antes que el por lo que podría no cumplirse el objetivo del SJN.

b) ¿Funciona correctamente con disciplina de señalización signal and wait? Justifique.
👀 Respuesta
Sí, la solución funciona correctamente con la disciplina de señalización Signal and Wait (S&W).
En esta disciplina, cuando un proceso ejecuta un signal, cede inmediatamente el control del monitor al proceso que fue despertado, el cual continúa su ejecución justo después del wait. El proceso que hizo el signal pasa a la cola de listos y debe esperar su turno para volver a ingresar al monitor.
Esto garantiza que el proceso con menor tiempo (según la política Shortest Job Next) —que estaba esperando con prioridad— será efectivamente el próximo en acceder al recurso, evitando que otro proceso pueda adelantarse y violar el orden deseado.
Por lo tanto, la política SJN se respeta correctamente bajo Signal and Wait, ya que se mantiene el control sobre el orden de ejecución de los procesos en espera.
📘 Definiciones complementarias:
- Signal and Continue: El proceso que ejecuta el
signalcontinúa usando el monitor, mientras que el proceso despertado debe competir por reingresar al monitor. - Signal and Wait: El proceso que ejecuta el
signalcede el monitor al proceso despertado, que continúa su ejecución justo después delwait.
📊 Comparación entre Signal and Continue vs Signal and Wait en SJN
| Aspecto | Signal and Continue (S&C) | Signal and Wait (S&W) |
|---|---|---|
¿Quién sigue ejecutando en el monitor después del signal? | El proceso que hizo el signal continúa. | El proceso que fue despertado entra inmediatamente al monitor. |
| Estado del proceso despertado | Pasa a la cola de listos y debe competir por reingresar al monitor. | Continúa inmediatamente dentro del monitor (no compite por el acceso). |
| Riesgo de pérdida de prioridad (SJN) | Alto: otro proceso puede ingresar antes que el de menor tiempo. | Nulo: se garantiza que el proceso con menor tiempo accede primero. |
| ¿Se respeta la política SJN? | ❌ No: puede no ejecutarse el proceso con menor tiempo debido a la competencia externa. | ✅ Sí: el proceso con menor tiempo es el próximo en continuar. |
| Uso recomendado en SJN | No recomendado, ya que puede romper la prioridad por tiempo. | Recomendado, ya que respeta el orden de espera basado en el tiempo. |
| Control de acceso | Depende del planificador del sistema operativo. | Controlado directamente por el monitor y su lógica de sincronización. |
2) “passing the condition” En Semaforos#
Utilice la técnica de “passing the condition” para implementar un semáforo fair usando monitores.
Codigo
monitor Semaforo {
int s = 1, espera = 0;
cond pos;
procedure P() {
if (s == 0) {
espera++;
wait(pos);
} else {
s = s - 1;
}
};
procedure V() {
if (espera == 0) {
s = s + 1;
} else {
espera--;
signal(pos);
}
};
};3) Problema de Concurrencia#
Sea “ocupados” una variable entera inicializada en N que representa la cantidad de slots ocupados de un buffer, y sean P1 y P2 dos programas que se ejecutan de manera concurrente, donde cada una de las instrucciones que los componen son atómicas.
| P1 | P2 |
|
|
¿El programa funciona correctamente para asegurar el manejo del buffer?
- Si su respuesta es afirmativa justifique.
- Sino, encuentre una secuencia de ejecución que lo verifique y escríbala, y además modifique la solución para que funcione correctamente (Suponga buffer, elemento_a_agregar y elemento_a_sacar variables declaradas).
Respuesta
No, el programa no funciona correctamente en un entorno concurrente.
🔍 Justificación con secuencia de ejecución:
Supongamos que el buffer está lleno (ocupados = N). En ese momento:
- El proceso P2 evalúa
if (ocupados > 0), lo cual es verdadero. - Luego, P2 ejecuta
ocupados := ocupados - 1, pero aún no ha leído el dato del buffer. - Justo después, el proceso P1 evalúa su condición
if (ocupados < N), que ahora también es verdadera, ya que P2 lo acaba de decrementar. - Entonces, P1 escribe en el buffer un nuevo valor, sobrescribiendo el dato que P2 todavía no alcanzó a leer.
⚠️ Como resultado, P2 pierde el dato original y lee un valor nuevo que no era el que debía consumir. Esto genera una condición de carrera (race condition) y un error de sincronización.
✅ Solución propuesta:
Para evitar este problema, es necesario postergar el decremento de ocupados en P2 hasta después de leer el valor del buffer, asegurando que el dato se consuma correctamente antes de liberar el espacio.
✔️ Código corregido de P2
if (ocupados > 0) then
begin
elemento_a_sacar := buffer;
ocupados := ocupados - 1;
end;Con esta corrección, P1 no podrá ingresar hasta que P2 haya terminado de leer el valor, manteniendo la coherencia del estado del buffer.
🧠 Nota adicional:
Este tipo de errores son comunes cuando no se usa un mecanismo de sincronización explícito, como semáforos, monitores o exclusión mutua. En un sistema real, lo ideal sería proteger el acceso al buffer con algún tipo de región crítica o control de concurrencia.
4) Problema de Concurrencia 2#
Sea “cantidad” una variable entera inicializada en 0 que representa la cantidad de elementos de un buffer, y sean P1 y P2 dos programas que se ejecutan de manera concurrente, donde cada una de las instrucciones que los componen son atómicas.
| P1 | P2 |
|
|
Además existen dos alumnos de concurrente que analizan el programa y opinan lo siguiente:
- “Pepe: este programa funciona correctamente ya que las instrucciones son atómicas”.
- “José: no Pepe estás equivocado, hay por lo menos una secuencia de ejecución en la cual funciona erróneamente”
¿Con cuál de los dos alumnos está de acuerdo? Si está de acuerdo con Pepe justifique su respuesta. Si está de acuerdo con José encuentre una secuencia de ejecución que verifique lo que José opina y escríbala, y modifique la solución para que funcione correctamente (Suponga buffer y elemento variables declaradas). (22-04-2009)
Resultado
✅ Estoy de acuerdo con José.
Aunque las instrucciones sean atómicas, el programa no es seguro concurrentemente, ya que existen interleavings (intercalaciones de ejecución) posibles que generan un comportamiento incorrecto.
🔍 Ejemplo de secuencia de ejecución errónea:
- El proceso P1 evalúa la condición
if (cantidad = 0)→ verdadera, y entra albegin. - P1 ejecuta la instrucción
cantidad := cantidad + 1, pero aún no ha escrito en el buffer. - En ese momento, el proceso P1 se interrumpe, y P2 toma el control.
- P2 evalúa
if (cantidad > 0)→ verdadera (porquecantidadahora vale 1). - P2 ejecuta
elemento_a_sacar := buffer, pero el buffer aún no fue actualizado por P1. - Como resultado, P2 lee un valor inválido o desactualizado del buffer.
⚠️ Problema identificado:
El hecho de que las instrucciones sean atómicas no garantiza la atomicidad de toda la sección crítica compuesta por múltiples instrucciones relacionadas entre sí.
✅ Modificación para que funcione correctamente:
Una forma de corregirlo es reordenar las instrucciones de P1, asegurando que el valor se escriba en el buffer antes de habilitar su lectura (es decir, antes de incrementar cantidad):
// P1 corregido:
if (cantidad = 0) then
begin
buffer := elemento_a_agregar;
cantidad := cantidad + 1;
end;De este modo, si P2 observa que cantidad > 0, entonces es seguro asumir que el buffer ya contiene un valor válido para ser consumido.
🧠 Conclusión:
Estoy de acuerdo con José, porque:
- El código original permite que P2 lea un valor inválido si se interrumpe a P1 en el momento inadecuado.
- La solución requiere ajustar el orden de operaciones para garantizar consistencia en el acceso al buffer, incluso si cada instrucción individual es atómica.
5) Indique los posibles valores finales de x#
Indique los posibles valores finales de x en el siguiente programa (justifique claramente su respuesta):
int x = 3;
sem s1 = 1, s2 = 0;
co
// P1
P(s1); // Espera mutex
x = x * x;
V(s1); // Libera mutex
// P2
P(s2); // Espera señal de P3
P(s1); // Espera mutex
x = x * 3;
V(s1);
// P3
P(s1); // Espera mutex
x = x - 2;
V(s2); // Señaliza a P2
V(s1);
ocs1 → mutex: puede pasar un solo proceso por vez.
s2 → semáforo de señalización: esperan señalización de un evento y pasa sólo uno.
Aunque se libere un semaforo, no tiene que volver a ejecutarse ya que no estamos en un while (Si un semaforo paso PASO)
Respuesta
| Orden de ejecución | Valor final de x |
|---|---|
| P1 → P3 → P2 | 21 |
| P3 → P2 → P1 | 9 |
| P3 → P1 → P2 | 3 |
P1 y P3 comienzan esperando a s1. Por ser un mutex, sólo puede continuar uno de ellos y no será interrumpido por el otro hasta liberar a s1.
Primer resultado
Si comienza P1:
- Asigna x=9
- luego incrementa s1 permitiendo que continúe P3.
- P3 asigna x=7 y señala s2.
- Esto habilita a P2 que estaba esperando.
- Si P2 continúa, intentará obtener s1 con lo cual se vuelve a bloquear volviendo el control a P3.
- En cualquier caso, P3 libera a s1 y termina.
- P2 es despertado, asigna x = 21 y termina.
- Valor final x=21.
Segundo y Tercer resultado
Si comienza P3:
- Asigna x = 1 y señala a s2.
- Esto habilita a P2 que estaba esperando.
- Si P2 continúa, intentará obtener s1 con lo cual se vuelve a bloquear volviendo el control a P3.
- Cuando P3 libera a s1, P1 y P2 pueden competir por él:
- Si gana P1:
- asigna x=1,
- libera a s1 y termina;
- finaliza P2 y asigna x = 3.
- Valor final x=3.
- Si gana P2:
- asigna x=3,
- libera a s1 y termina;
- finaliza P1 y asigna x = 9.
- Valor final x = 9.
- Si gana P1:
P2 nunca puede comenzar la historia ya que espera un semáforo de señalización que sólo P3 señala. Cualquier historia en la que P2 esté antes de P3 es inválida. En todas las historias los semáforos terminan con los mismos valores con los que están inicializados.
6) Cuales valores de k son posibles#
c) Dado el siguiente programa concurrente indique cuáles valores de K son posibles al finalizar, y describa una secuencia de instrucciones para obtener dicho resultado:
Process P1 {
for (i = 1 to K) {
N = N + 1;
}
}
Process P2 {
for (i = 1 to K) {
N = N + 1;
}
}i) 2K
ii) 2K + 2
iii) K
iv) 2
Respuesta
// Ambos procesos ejecutan el mismo bucle:
for (i = 1 to K)
N = N + 1;✅ i) Valor final = 2K
Caso posible: ejecución secuencial sin interferencia.
Ejemplo (K = 3):
P1: N=0 -> 1 -> 2 -> 3
P2: N=3 -> 4 -> 5 -> 6
Resultado final: N = 6 = 2*K❌ ii) Valor final = 2K + 2
Caso imposible.
Justificación:
Cada proceso ejecuta exactamente K incrementos. Como mucho se pueden hacer 2K sumas. No hay forma de hacer más sin ejecutar más iteraciones, lo cual no ocurre.
✅ iii) Valor final = K
Caso posible: interferencia total entre procesos. Se pisan las operaciones.
Ejemplo (K = 3):
N inicialmente = 0
Intercalado:
P1 lee N=0 // aún no actualiza
P2 lee N=0 // aún no actualiza
P1 escribe N=1
P2 escribe N=1 // pisa el valor anterior → se pierde un incremento
Repite este patrón durante las 3 iteraciones.
Resultado final: solo 3 incrementos efectivos → N = 3 = K✅ iv) Valor final = 2
Caso posible: interferencia total y mal intercalado extremo.
Ejemplo (K = 3):
N = 0
P1 iteración 1: lee N=0
P2 iteración 1: lee N=0
P1 escribe N=1
P2 escribe N=1 → pisa a P1
P1 iteración 2: lee N=1
P2 iteración 2: lee N=1
P1 escribe N=2
P2 escribe N=2 → pisa a P1
Resultado final: N = 2🚨 Rezar para que no Tomen#

1) Resuelva con monitores#
Resuelva con monitores el siguiente problema:
Tres clases de procesos comparten el acceso a una lista enlazada: searchers, inserters y deleters.
- Los searchers sólo examinan la lista, y por lo tanto pueden ejecutar concurrentemente unos con otros.
- Los inserters agregan nuevos ítems al final de la lista; las inserciones deben ser mutuamente exclusivas para evitar insertar dos ítems casi al mismo tiempo. Sin embargo, un insert puede hacerse en paralelo con uno o más searchers.
- Por último, los deleters remueven ítems de cualquier lugar de la lista. A lo sumo un deleter puede acceder la lista a la vez, y el borrado también debe ser mutuamente exclusivo con searchers e inserters.
Codigo
monitor Controlador_ListaEnlazada {
int numSearchers = 0, numInserters = 0, numDeleters = 0;
cond searchers, inserters, deleters;
procedure pedir_Deleter() {
while (numSearchers > 0 OR numInserters > 0 OR numDeleters > 0) {
wait(deleters);
}
numDeleters = numDeleters + 1;
}
procedure liberar_Deleter() {
numDeleters = numDeleters - 1;
signal(inserters);
signal(deleters);
signal_all(searchers);
}
procedure pedir_Searcher() {
while (numDeleters > 0) {
wait(searchers);
}
numSearchers = numSearchers + 1;
}
procedure liberar_Searcher() {
numSearchers = numSearchers - 1;
if (numSearchers == 0 AND numInserters == 0) {
signal(deleters);
}
}
procedure pedir_Inserter() {
while (numDeleters > 0 OR numInserters > 0) {
wait(inserters);
}
numInserters = numInserters + 1;
}
procedure liberar_Inserter() {
numInserters = numInserters - 1;
signal(inserters);
if (numSearchers == 0) {
signal(deleters);
}
}
}🧵 Procesos:
process Searchers[i = 1..S] {
Controlador_ListaEnlazada.pedir_Searcher();
<Realiza búsqueda en la lista>
Controlador_ListaEnlazada.liberar_Searcher();
}
process Inserters[j = 1..I] {
Controlador_ListaEnlazada.pedir_Inserter();
<Inserta en la lista>
Controlador_ListaEnlazada.liberar_Inserter();
}
process Deleters[k = 1..D] {
Controlador_ListaEnlazada.pedir_Deleter();
<Borra en la lista>
Controlador_ListaEnlazada.liberar_Deleter();
}🧠 Resumen: Monitor Controlador_ListaEnlazada
👥 Tipos de procesos:
- Searchers: pueden acceder concurrentemente, salvo que haya un Deleter.
- Inserters: acceden de a uno, pero pueden convivir con Searchers.
- Deleters: requieren exclusión total (no pueden ejecutarse junto a ningún otro proceso).
🔒 Comportamiento de sincronización:
Searchersesperan si hay unDeleter.Insertersesperan si hay otroInsertero unDeleter.Deletersesperan si hay cualquier otro proceso activo (Searcher o Inserter).- Al liberar, se despiertan procesos bloqueados según condiciones.
✅ ¿Funciona correctamente? Sí, el monitor implementa correctamente las restricciones de sincronización para los tres tipos de procesos. Asegura exclusión mutua, convivencia segura y respeta la lógica de prioridades.
2) Protocolos de Acceso a la SC#
En los protocolos de acceso a sección crítica vistos en clase, cada proceso ejecuta el mismo algoritmo. Una manera alternativa de resolver el problema es usando un proceso coordinador. En este caso, cuando cada proceso SC[i] quiere entrar a su sección crítica le avisa al coordinador, y espera a que éste le dé permiso. Al terminar de ejecutar su sección crítica, el proceso SC[i] le avisa al coordinador.
Desarrolle protocolos para los procesos SC[i] y el coordinador usando sólo variables compartidas (no tenga en cuenta la propiedad de eventual entrada).
Respuesta
int aviso[1:N] = ([N] 0), permiso[1:N] = ([N] 0);
|
|
3) Solución a la Criba#
💀 Dudo mucho que tomen este ejercicio, lo pongo por las dudas
Describa la solución utilizando la criba de Eratóstenes al problema de hallar los primos entre 2 y n. ¿Cómo termina el algoritmo? ¿Qué modificaría para que no termine de esa manera?
Codigo
La criba de Eratóstenes es un algoritmo clásico para determinar cuáles números en un rango son primos. Supongamos que queremos generar todos los primos entre 2 y n. Primero, escribimos una lista con todos los números:
2 3 4 5 6 7 ... nComenzando con el primer número no tachado en la lista, 2, recorremos la lista y borramos los múltiplos de ese número. Si n es impar, obtenemos la lista:
2 3 5 7 ... nEn este momento, los números borrados no son primos; los números que quedan todavía son candidatos a ser primos. Pasamos al próximo número, 3, y repetimos el anterior proceso borrando los múltiplos de 3. Si seguimos este proceso hasta que todo número fue considerado, los números que quedan en la lista final serán todos los primos entre 2 y n.
Para solucionar este problema de forma paralela podemos emplear un pipeline de procesos filtro.
- Cada filtro recibe una serie de números de su predecesor y envía una serie de números a su sucesor.
- El primer número que recibe un filtro es el próximo primo más grande;
- Le pasa a su sucesor todos los números que no son múltiplos del primero.
El siguiente es el algoritmo pipeline para la generación de números primos.
Por cada canal, el primer número es primo y todos los otros números no son múltiplo de ningún primo menor que el primer número:
Process Criba[1]
{
int p = 2;
for [i = 3 to n by 2]
Criba[2] ! (i);
}
Process Criba[i = 2 to L]
{
int p, proximo;
Criba[i-1] ? p;
do Criba[i-1] ? (proximo) →
if ((proximo MOD p) <> 0) →
Criba[i+1] ! (proximo);
fi
od
}- El primer proceso, Criba[1], envía todos los números impares desde
3 a na Criba[2]. - Cada uno de los otros procesos recibe una serie de números de su predecesor.
- El primer número
pque recibe el procesoCriba[i]es el i-ésimo primo. - Cada Criba[i] subsecuentemente pasa todos los otros números que recibe que no son múltiplos de su primo
p. - El número total
Lde procesos Cribe debe ser lo suficientemente grande para garantizar que todos los primos hastanson generados. Por ejemplo, hay 25 primos menores que 100; - el porcentaje decrece para valores crecientes de
n.
El programa anterior termina en deadlock, ya que no hay forma de saber cuál es el último número de la secuencia y cada proceso queda esperando un próximo número que no llega.
Podemos fácilmente modificarlo para que termine normalmente usando centinelas, es decir que al final de los streams de entrada son marcados por un centinela
# EOS: End Of Stream (-1 indica fin del flujo)
Process Criba[1] {
int p = 2;
# Enviar todos los números impares desde 3 hasta n a Criba[2]
for [i = 3 to n by 2]
Criba[2] ! i;
# Enviar fin de flujo
Criba[2] ! -1;
}
Process Criba[i = 2 to L] {
int p, proximo;
boolean seguir = true;
# Recibe el primer número (primo)
Criba[i-1] ? p;
do (seguir);
# Recibe siguiente candidato
Criba[i-1] ? proximo ->
if (proximo = -1) {
seguir = false;
Criba[i+1] ! -1; # Propaga EOS al siguiente proceso
}
else if ((proximo MOD p) <> 0) {
Criba[i+1] ! proximo; # Si no es múltiplo, lo pasa
}
od
}4) Transformar Solucion usando mensajes asincronicos#
Dada la siguiente solución con monitores al problema de alocación de un recurso con múltiples unidades, transforme la misma en una solución utilizando mensajes asincrónicos.
Monitor Alocador_Recurso {
INT disponible = MAXUNIDADES;
SET unidades = valores iniciales;
COND libre; // TRUE cuando hay recursos
procedure adquirir(INT id) {
if (disponible == 0)
wait(libre);
else {
disponible = disponible - 1;
remove(unidades, id);
}
}
procedure liberar(INT id) {
insert(unidades, id);
if (empty(libre))
disponible := disponible + 1;
else
signal(libre);
}
}Respuesta
type clase_op = enum(adquirir, liberar);
chan request(int idCliente, claseOp oper, int idUnidad);
chan respuesta[n](int id_unidad);
Process Administrador_Recurso {
int disponible = MAXUNIDADES;
set unidades = valor inicial disponible;
queue pendientes;
while (true) {
receive request(idCliente, oper, id_unidad);
if (oper == adquirir) {
if (disponible > 0) {
disponible = disponible - 1;
remove(unidades, id_unidad);
send respuesta[idCliente](id_unidad);
} else {
insert(pendientes, idCliente);
}
} else {
if (empty(pendientes)) {
disponible = disponible + 1;
insert(unidades, id_unidad);
} else {
remove(pendientes, idCliente);
send respuesta[idCliente](id_unidad);
}
}
}
}
// Fin del proceso Administrador_Recurso
Process Cliente[i = 1 to n] {
int id_unidad;
send request(i, adquirir, 0);
receive respuesta[i](id_unidad);
// Usa la unidad
send request(i, liberar, id_unidad);
}🧠 1. Modelo de comunicación
-
Monitores utilizan una comunicación directa entre procesos a través de procedimientos compartidos. El proceso cliente entra al monitor, ejecuta
adquirir()oliberar(), y bloquea su ejecución si no puede continuar (por ejemplo, si no hay recursos). -
Mensajes asincrónicos, en cambio, se basan en comunicación por paso de mensajes. El cliente envía un mensaje al administrador (
request) y luego espera la respuesta por otro canal (respuesta[i]). No hay acceso directo a las variables compartidas; todo se coordina mediante mensajes.
🔁 2. Sincronización y control de acceso
-
En el monitor, la sincronización es implícita: si
disponible == 0, el proceso ejecutawait(libre)y queda suspendido automáticamente hasta que otro proceso hagasignal(libre)al liberar un recurso. -
En la versión con mensajes, no hay suspensión automática. El administrador debe mantener una cola de espera (
pendientes) y decidir manualmente a quién responder y cuándo. Si alguien libera una unidad y hay clientes esperando, el administrador desencola y responde explícitamente.
🔐 3. Visibilidad y consistencia del estado
-
En el monitor, los procesos tienen acceso directo a las variables
disponible,unidades, etc., pero solo uno a la vez, garantizando exclusión mutua. -
Con mensajes asincrónicos, solo el administrador conoce y modifica el estado global. Los clientes no ven directamente cuántos recursos quedan; solo saben si obtuvieron uno o no, cuando reciben la respuesta.
🧩 4. Modelo de espera
-
En monitores, la espera se maneja con
waitysignal, que pueden funcionar según dos disciplinas:- Signal and Wait (el proceso que señala cede el monitor al despertado)
- Signal and Continue (el proceso que señala continúa)
-
En mensajes, la espera es activa y manual: el cliente se bloquea esperando una respuesta, y el administrador debe tener lógica para enviarle esa respuesta cuando le toque.
⚙️ 5. Aplicabilidad según arquitectura
-
Los monitores son más adecuados para sistemas centralizados o con memoria compartida, ya que dependen de sincronización interna y acceso directo a variables.
-
Los mensajes asincrónicos son ideales en sistemas distribuidos o clusters, donde no existe memoria compartida y cada proceso corre en su propio nodo. Permiten separar cómputo y comunicación y escalar fácilmente.
💬 Ejemplo concreto
Supongamos que hay 3 unidades disponibles, y 5 procesos piden recursos.
-
En el monitor, los 3 primeros entran y adquieren recursos; los otros 2 quedan bloqueados con
wait(libre)hasta que alguien libere. Luego,liberar()hacesignal()y despierta a uno. -
En la versión con mensajes, los 3 primeros reciben respuesta del administrador inmediatamente. Los otros 2 son enviados a la cola
pendientes, y recién serán atendidos cuando un recurso sea liberado y el administrador procese esa cola.
✅ Conclusión
- El uso de monitores es más directo y automatizado, pero menos flexible fuera de sistemas con memoria compartida.
- El enfoque de mensajes asincrónicos permite mayor control y distribución, pero requiere manejar manualmente colas, lógica de respuesta y sincronización, lo cual lo hace más complejo pero también más escalable.
5) Problema de ordenar de menor a mayor un arreglo#
Sea el problema de ordenar de menor a mayor un arreglo de A[1..n]
1. Escriba un programa donde dos procesos (cada uno con n/2 valores) realicen la operación en paralelo mediante una serie de intercambios.
|
|
2. ¿Cuántos mensajes intercambian en el mejor de los casos? ¿Y en el peor de los casos?
Mejor caso:
En el escenario más favorable, los arreglos ya están correctamente distribuidos:
- Los
n/2valores más pequeños están en el proceso P1. - Los
n/2valores más grandes están en P2.
Como los extremos (mayor de a1 y menor de a2) ya están en orden, los procesos solo necesitan hacer una comparación inicial y confirmar que no hay que intercambiar nada.
Resultado: Solo se envían 2 mensajes:
- P1 envía su mayor a P2.
- P2 responde con su menor a P1.
🧪 Ejemplo con n = 6 (a1 y a2 de tamaño 3)
Supongamos:
P1: a1 = [1, 2, 3] (valores más chicos)
P2: a2 = [4, 5, 6] (valores más grandes)- Proceso:
1)P1 envía el mayor dea1:32)P2 envía el menor dea2:43)P1 verifica:3 < 4✅, así que todo está ordenado
- ✅ Resultado:
- Se intercambian 2 mensajes:
3 →,4 → - No se modifica nada
- Se intercambian 2 mensajes:
Peor caso:
En el peor de los casos, todos los elementos están en el proceso equivocado:
- Es decir, los mayores están en P1 y los menores en P2.
Esto obligará a intercambiar completamente los n/2 elementos entre ambos procesos.
Cada valor necesita un mensaje de ida y uno de vuelta, ya que el intercambio es coordinado y requiere validación mutua.
Resultado: Se intercambian n mensajes:
n/2valores de P1 a P2n/2valores de P2 a P1 → total:(n/2) * 2 = nmensajes
Supongamos:
P1: a1 = [6, 5, 4] (valores grandes, mal ubicados)
P2: a2 = [3, 2, 1] (valores chicos, mal ubicados)- Proceso:
- P1 envía su mayor
6, P2 su menor1 - Ambos comparan y detectan que los elementos están desordenados, por lo tanto empiezan a intercambiar valores de uno en uno.
- P1 envía su mayor
- Intercambios:
-
6↔1
-
5↔2
-
4↔3
-
Cada par requiere 2 mensajes (ida y vuelta).
✅ Resultado:
- Se hacen 3 intercambios
- Se envían 6 mensajes (3 * 2)
📊 Resumen final:
| Caso | Cantidad de mensajes | Explicación breve |
|---|---|---|
| Mejor caso | 2 | Solo se comparan los extremos, no se intercambia nada |
| Peor caso | n | Se intercambian todos los valores (n/2 * 2 = n) |
3. Utilice la idea de 1), extienda la solución a K procesos, con n/k valores c/u (“odd-even-exchange sort”).
Asumimos que existen n procesos P[1:n] y que n es par. Cada proceso ejecuta una serie de rondas. En las rondas impares, los procesos impares P[odd] intercambian valores con el siguiente proceso impar P[odd+1] si el valor esta fuera de orden. En rondas pares, los procesos pares P[even] intercambia valores con el siguiente proceso par P[even+1] si los valores estan fuera de orden. P[1] y P[n] no hacen nada en las rondas pares.
Respuesta
process Proc[i = 1..k] {
int a[1..n/k]; // subarreglo local ordenado
int dato;
const min = 1;
const max = n/k;
ordenar_localmente(a); // ordenar el arreglo local al iniciar
for ronda = 1 to k {
// Si la ronda y el índice tienen la misma paridad: proceso actúa como EMISOR
if (i mod 2 == ronda mod 2 and i < k) {
// Enviar el mayor valor local al vecino derecho
send(proc[i+1], a[max]);
receive(proc[i+1], dato);
while (a[max] > dato) {
// Insertar el dato recibido ordenadamente en 'a', descartando el mayor
insertar_en_orden(a, dato);
send(proc[i+1], a[max]);
receive(proc[i+1], dato);
}
}
// Si la ronda y el índice tienen distinta paridad: proceso actúa como RECEPTOR
if (i mod 2 != ronda mod 2 and i > 1) {
receive(proc[i-1], dato);
send(proc[i-1], a[min]);
while (a[min] < dato) {
// Insertar el dato recibido ordenadamente en 'a', descartando el menor
insertar_en_orden(a, dato);
receive(proc[i-1], dato);
send(proc[i-1], a[min]);
}
}
}
}Lo de abajo no hace falta pero es para probar
Con k = 4 procesos y n = 8 valores, llevando las rondas hasta que los valores queden totalmente ordenados globalmente.
Configuración inicial
Cada proceso tiene 2 elementos (n/k = 2), ordenados localmente:
| Proceso | Valores iniciales |
|---|---|
| P1 | [8, 9] |
| P2 | [5, 7] |
| P3 | [3, 6] |
| P4 | [1, 4] |
Rondas del algoritmo (hasta que esté ordenado)
| Ronda | Procesos activos | Cambios realizados | Estado final por proceso |
|---|---|---|---|
| 0 | — | — | P1: [8, 9], P2: [5, 7], P3: [3, 6], P4: [1, 4] |
| 1 | P1↔P2, P3↔P4 | P1⇄P2: 9⇄5 → P1: [5, 8], P2: [7, 9] P3⇄P4: 6⇄1 → P3: [1, 3], P4: [4, 6] | P1: [5, 8], P2: [7, 9], P3: [1, 3], P4: [4, 6] |
| 2 | P2↔P3 | 9⇄1 → P2: [1, 7], P3: [3, 9] | P1: [5, 8], P2: [1, 7], P3: [3, 9], P4: [4, 6] |
| 3 | P1↔P2, P3↔P4 | 8⇄1 → P1: [1, 5], P2: [7, 8]; 9⇄4 → P3: [3, 4], P4: [6, 9] | P1: [1, 5], P2: [7, 8], P3: [3, 4], P4: [6, 9] |
| 4 | P2↔P3 | 8⇄3 → P2: [3, 7], P3: [4, 8] | P1: [1, 5], P2: [3, 7], P3: [4, 8], P4: [6, 9] |
| 5 | P1↔P2, P3↔P4 | 5⇄3 → P1: [1, 3], P2: [5, 7]; 8⇄6 → P3: [4, 6], P4: [8, 9] | P1: [1, 3], P2: [5, 7], P3: [4, 6], P4: [8, 9] |
| 6 | P2↔P3 | 7⇄4 → P2: [4, 5], P3: [6, 7] | P1: [1, 3], P2: [4, 5], P3: [6, 7], P4: [8, 9] |
| 7 | P1↔P2, P3↔P4 | No intercambios necesarios (valores ya ordenados) | P1: [1, 3], P2: [4, 5], P3: [6, 7], P4: [8, 9] |
P1: [1, 3]
P2: [4, 5]
P3: [6, 7]
P4: [8, 9]
→ Resultado final: [1, 3, 4, 5, 6, 7, 8, 9]El arreglo quedó completamente ordenado tras 7 rondas, que coincide con el peor caso esperado (hasta k rondas).
b. ¿Cuántos mensajes intercambian en 3) en el mejor caso? ¿Y en el peor de los casos?
Respuesta
Si cada proceso ejecuta suficientes rondas para garantizar que la lista estará ordenada (en general, al menos k rondas), en el k-proceso, cada uno intercambia hasta (n/k)+1 mensajes por ronda. El algoritmo requiere hasta k^2 * (n/k+1).
Se puede usar un proceso coordinador al cual todos los procesos le envían en cada ronda si realizaron algún cambio o no.
Si al recibir todos los mensajes el coordinador detecta que ninguno cambio nada les comunica que terminaron.
Esto agrega overhead de mensajes ya que se envían mensajes al coordinador y desde el coordinador. Con n procesos tenemos un overhead de 2*k mensajes en cada ronda.
Nota: Utilice un mecanismo de pasaje de mensajes, justifique la elección del mismo.
PMS es más adecuado en este caso porque los procesos deben sincronizar de a pares en cada ronda por lo que PMA no sería tan útil para la resolución de este problema ya que se necesitaría implementar una barrera simétrica para sincronizar los procesos de cada etapa.
6) Problema de ordenar de menor a mayor 2#
Suponga los siguientes métodos de ordenación de menor a mayor para n valores (n par y potencia de 2), utilizando pasaje de mensajes:
- 1) Un pipeline de filtros. El primero hace input de los valores de a uno por vez, mantiene el mínimo y le pasa los otros al siguiente. Cada filtro hace lo mismo: recibe un stream de valores desde el predecesor, mantiene el más chico y pasa los otros al sucesor.
- 2) Una red de procesos filtro (como la de la figura).
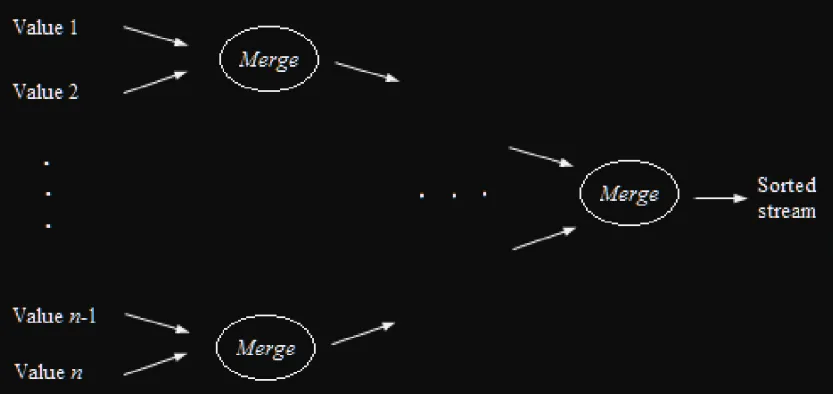
- 3) Odd/even exchange sort. Hay n procesos P[1:n], Cada uno ejecuta una serie de rondas. En las rondas “impares”, los procesos con número impar P[impar] intercambian valores con P[impar+1]. En las rondas “pares”, los procesos con número par P[par] intercambian valores con P[par+1] (P[1] y P[n] no hacen nada en las rondas “pares”). En cada caso, si los números están desordenados actualizan su valor con el recibido.
Asuma que cada proceso tiene almacenamiento local sólo para dos valores (el próximo y el mantenido hasta ese momento).
a) ¿Cuántos procesos son necesarios en 1 y 2? Justifique.
Respuesta
Para la alternativa del pipeline de filtros, se requieren n procesos, ya que cada uno actúa como un filtro que retiene el valor mínimo recibido hasta el momento y envía los valores mayores al siguiente. Como se desea ordenar n elementos y cada proceso retiene uno, se necesitan n procesos para que todos los valores queden almacenados, uno en cada proceso, en orden ascendente.
En cambio, para la alternativa de la red de procesos filtro (basada en una estructura de árbol binario), se necesitan n - 1 procesos. Esto se debe a que los valores iniciales están en las hojas del árbol (hay n hojas), y los nodos internos se encargan de ir fusionando pares de valores o secuencias. En un árbol binario completo con n hojas, hay exactamente n - 1 nodos internos. Por lo tanto, se requieren n - 1 procesos de merge para combinar todos los valores en una única secuencia ordenada.
Perfecto, Fabián. A continuación te doy un ejemplo para cada alternativa (pipeline de filtros y red de merges) con n = 4 valores (potencia de 2) y su tabla de ejecución correspondiente para que visualices cómo se comportan ambos métodos.
📌 Ejemplo 1: Pipeline de filtros
Idea: Cada proceso filtra el mínimo de los valores que recibe y pasa el resto al siguiente.
Valores iniciales: 6, 2, 8, 4 (se envían en ese orden)
Estructura:
Entrada → P1 → P2 → P3 → P4Tabla de ejecución
| Paso | Valor recibido | P1 | P2 | P3 | P4 |
|---|---|---|---|---|---|
| 1 | 6 | 6 | — | — | — |
| 2 | 2 | 2 (↓6) | 6 | — | — |
| 3 | 8 | 2 (↓8) | 6 (↓8) | 8 | — |
| 4 | 4 | 2 (↓4) | 4 (↓6) | 6 (↓8) | 8 |
Resultado final:
P1: 2
P2: 4
P3: 6
P4: 8
→ [2, 4, 6, 8] (ordenado)
Procesos necesarios: 4 (uno por cada valor)
📌 Ejemplo 2: Red de merges (filtros)
Idea: Se usan procesos que combinan pares de valores en orden. Cada proceso mergea dos entradas ordenadas y produce una salida ordenada.
Valores iniciales (en hojas):
Entrada a M1: 6 y 2
Entrada a M2: 8 y 4
Estructura:
Nivel 0: 6 2 8 4
\ / \ /
Nivel 1: M1 M2
\ /
Nivel 2: M3Tabla de ejecución
| Merge | Entrada izq | Entrada der | Salida ordenada |
|---|---|---|---|
| M1 | 6 | 2 | [2, 6] |
| M2 | 8 | 4 | [4, 8] |
| M3 | [2, 6] | [4, 8] | [2, 4, 6, 8] |
Procesos necesarios:
- 3 merges → n − 1 = 3 procesos
📋 Comparación en tabla
| Método | Valores iniciales | Nº de procesos | Resultado final | Observaciones |
|---|---|---|---|---|
| Pipeline de filtros | 6, 2, 8, 4 | 4 | [2, 4, 6, 8] | Cada proceso retiene uno; paso a paso |
| Red de merges | 6, 2, 8, 4 | 3 | [2, 4, 6, 8] | Requiere mergear en árbol binario completo |
b) ¿Cuántos mensajes envía cada algoritmo para ordenar los valores? Justifique.
Respuesta
📌 Pipeline
A cada proceso se le asigna un número del 1 al n, y los valores se envían uno por uno al primer proceso.
- El proceso 1 recibe
nvalores, se queda con el menor y envían−1al proceso 2. - El proceso 2 recibe
n−1valores, se queda con el menor y envían−2al proceso 3. - …
- El proceso n recibe 1 valor y no envía ninguno.
La cantidad total de mensajes enviados entre procesos es:

A esto se le suman n mensajes EOS (End Of Stream), ya que cada proceso necesita saber cuándo detenerse. Por lo tanto:

📌 Red de procesos filtro (merge tree)
En este caso, con n valores a ordenar y una red de log₂(n) niveles, la cantidad de mensajes de combinación es:
![]()
Esto incluye las comparaciones y fusiones realizadas en cada nivel del árbol.
Además, se deben sumar:
nmensajes para enviar los valores desde los nodos hoja (datos iniciales).n − 1mensajes EOS desde los nodos internos al superior para finalizar.
![]()
📌 Odd/Even Exchange Sort
Si cada proceso ejecuta suficientes rondas para garantizar el orden (en general, hasta k rondas con k procesos), entonces en cada ronda cada proceso intercambia hasta:
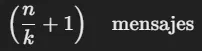
Cada intercambio requiere dos mensajes (ida y vuelta), y se repite durante k rondas, así que el total de mensajes es:
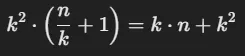
Resumen de todos los resultados

- En el Pipeline, cada proceso filtra y pasa el resto, por lo que la cantidad de mensajes crece cuadráticamente.
- En la Red de filtros (árbol de merges), el ordenamiento sigue una estructura logarítmica. Muy eficiente para merges en paralelo.
- En el Odd/Even, el ordenamiento depende de la cantidad de rondas (
k), y aunque es simple de implementar, puede requerir muchos mensajes si los datos están muy desordenados.
c) ¿En cada caso, cuáles mensajes pueden ser enviados en paralelo (asumiendo que existe el hardware apropiado) y cuáles son enviados secuencialmente? Justifique.
Respuesta
-
Pipeline de filtros:
Una vez que el pipeline está lleno, es posible enviar mensajes en paralelo entre todos los procesos del pipeline. Cada proceso está recibiendo, procesando y enviando valores simultáneamente. Por lo tanto, en un instante dado, pueden enviarse en paralelo hastanmensajes (uno por cada proceso). Al inicio y al final, el envío es más secuencial, pero en régimen estable, el flujo es completamente paralelo. -
Red de procesos filtro (merge tree):
En esta estructura, los mensajes pueden enviarse en paralelo a nivel de cada capa del árbol. Cada proceso del mismo nivel actúa de forma independiente, por lo que se pueden enviar hastan / 2,n / 4, …,1mensajes en paralelo según el nivel. El envío entre niveles debe ser secuencial (los procesos de un nivel deben esperar los resultados del anterior). -
Odd/Even Exchange Sort:
En cada ronda (par o impar), todos los procesos que participan pueden enviar mensajes en paralelo. Por ejemplo, en una ronda impar, todos los procesos con índice impar se comunican simultáneamente con sus vecinos. Por lo tanto, en cada ronda puede haber hastan/2mensajes en paralelo.
📋 Comparación: Paralelismo en el envío de mensajes
| Método | Paralelismo posible | Secuencialidad obligatoria | Observaciones clave |
|---|---|---|---|
| Pipeline de filtros | Hasta n mensajes por instante (una vez lleno) | Inicio (pipeline vacío) y último paso | Cada proceso recibe, filtra y reenvía simultáneamente |
| Red de merges (filtros) | Hasta n / 2, n / 4, …, 1 por nivel del árbol | Entre niveles del árbol | Dentro de un mismo nivel: procesos trabajan en paralelo |
| Odd/Even Exchange Sort | Hasta n / 2 mensajes por ronda | Rondas ejecutadas secuencialmente | En cada ronda, procesos con mismo tipo (par/impar) se comunican |
d) ¿Cuál es el tiempo total de ejecución de cada algoritmo? Asuma que cada operación de comparación o de envío de mensaje toma 1 una unidad de tiempo. Justifique.
Respuesta
📌 Algoritmo 1: Pipeline de filtros
Cada mensaje enviado implica una comparación y luego el envío (2 unidades de tiempo).
En el punto (a) se determinó que se envían
![]()
Por lo tanto, el tiempo total es:
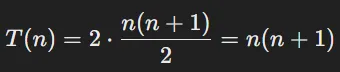
Entonces:
![]()
📌 Algoritmo 2: Red de procesos filtro (árbol de merges)
Cada mensaje también implica 1 comparación y 1 envío → 2 unidades por mensaje.
Ya vimos que se envían
![]()
Entonces:
![]()
📌 Algoritmo 3: Odd/Even Exchange Sort
- En cada ronda, cada proceso:
- Hace una comparación (1)
- Envía un mensaje (1)
- Recibe un mensaje (1)
- Asigna/intercambia valores (1)
→ Total = 4 unidades por proceso por ronda
- En el peor caso, se necesitan hasta
nrondas. - Entonces:
![]()
Acomodando la tabla final
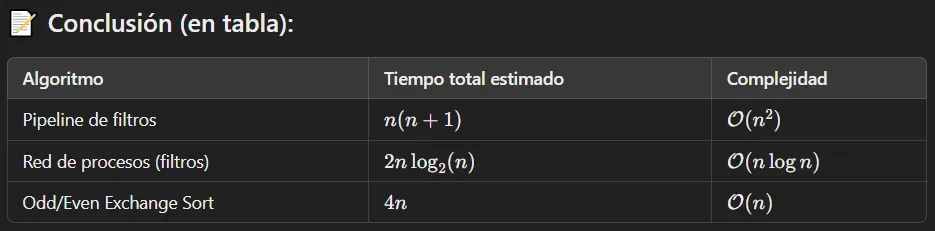
Tabla final
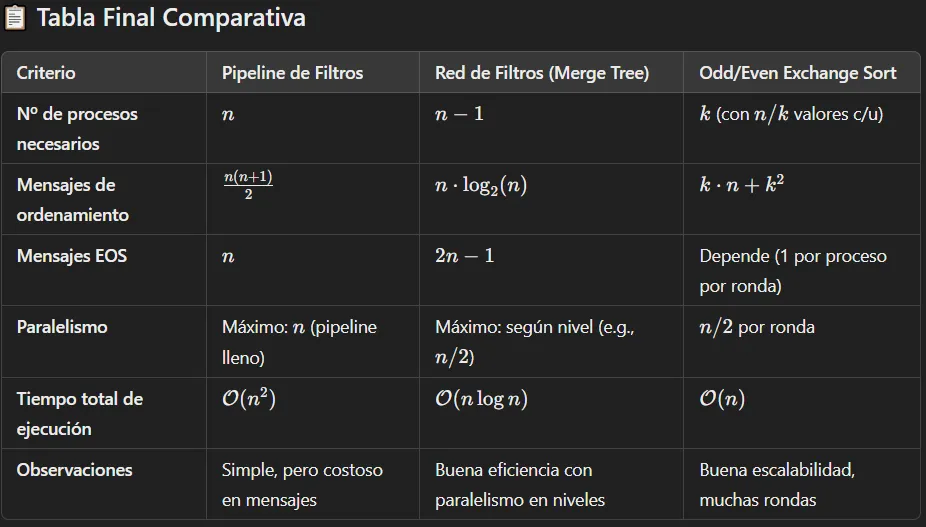
7) Suponga que un proceso productor y n procesos consumidores#
(Broadcast atómico). Suponga que un proceso productor y n procesos consumidores comparten un buffer unitario. El productor deposita mensajes en el buffer y los consumidores los retiran. Cada mensaje depositado por el productor tiene que ser retirado por los n consumidores antes de que el productor pueda depositar otro mensaje en el buffer.
a) Desarrolle una solución utilizando semáforos.
sem depositar := 1;
sem retirar := 1;
sem consumi[n] := ([n] 0);
int cant_consumido := ([n] 0);
T buffer;
process productor {
while (true) {
P(depositar);
buffer := generarDato(); // Devuelve un entero para el buffer
cant_consumido := 0;
for i to n do
V(consumi[i]);
}
}
process consumidor[i = 1..n] {
T dato;
while (true) {
P(consumi[i]); // Espero que el dato esté en el buffer
P(retirar); // Espero para tener acceso al buffer
dato := buffer;
cant_consumido++;
if (cant_consumido == n)
V(depositar);
V(retirar);
}
}🎯 Objetivo
El productor debe generar un dato y colocarlo en un buffer compartido.
Cada consumidor debe leer ese dato una única vez.
Solo cuando todos lo hayan leído, el productor podrá colocar un nuevo dato.
🧩 Supuestos para el ejemplo
- Hay
n = 2consumidores:C1yC2 - El buffer inicialmente está vacío
- El productor genera números enteros:
1,2,3, etc.
🔄 Ejecución paso a paso
🔹 Estado inicial
| Variable | Valor inicial |
|---|---|
depositar | 1 |
retirar | 1 |
consumi[1] | 0 |
consumi[2] | 0 |
cant_consumido | 0 |
buffer | vacío |
⏱ Paso 1: El productor genera un dato
P(depositar)→ pasa (vale 1)buffer := generarDato() → 1cant_consumido := 0V(consumi[1])→consumi[1] = 1V(consumi[2])→consumi[2] = 1
🔁 El productor queda esperando a que los 2 consumidores consuman antes de generar otro dato.
⏱ Paso 2: El consumidor 1 consume
P(consumi[1])→ pasaP(retirar)→ pasa (vale 1)dato := buffer = 1cant_consumido := 1cant_consumido != n → no hace nadaV(retirar)→retirar = 1
⏱ Paso 3: El consumidor 2 consume
P(consumi[2])→ pasaP(retirar)→ pasadato := buffer = 1cant_consumido := 2cant_consumido == n→ entoncesV(depositar)→ ahora el productor puede seguirV(retirar)
⏱ Paso 4: El productor continúa
P(depositar)→ pasa (porque fue liberado)buffer := 2cant_consumido := 0V(consumi[1]),V(consumi[2])→ y sigue el ciclo
✅ Garantías del algoritmo
| Propiedad | Cumple |
|---|---|
| Exclusión mutua en acceso | ✅ |
| Cada consumidor lee una vez | ✅ |
| Productor espera a todos | ✅ |
| No hay pérdida de datos | ✅ |
b) Suponga que el buffer tiene b slots. El productor puede depositar mensaje sólo en slots vacíos y cada mensaje tiene que ser recibido por los n consumidores antes de que el slot pueda ser reusado. Además, cada consumidor debe recibir los mensajes en el orden en que fueron depositados (note que los distintos consumidores pueden recibir los mensajes en distintos momentos siempre que los reciban en orden).
Extienda la respuesta dada en a) para resolver este problema más general.
Respuesta
sem retirar[tamBuffer] := 1; // semáforo para cada slot del buffer
sem consumir[n] := ([n] 0);
int cant_consumido[tamBuffer] := ([n] 0);
T buffer[tamBuffer];
process productor {
int posLibre := 0; // Siguiente posición libre del buffer (productor)
while(true){
P(depositar);
buffer[posLibre] := generarDato(); // Devuelve dato tipo T para el buffer
cant_consumido[posLibre] := 0;
for i to n do
V(consumir[i]);
posLibre := (posLibre + 1) mod n;
}
}
process consumidor[i: 1..n] {
int post_actual := 0; // Slot del que debe consumir
T dato;
while(true){
P(consumir[i]);
P(retirar[post_actual]); // Espera por un slot en particular
dato := buffer[post_actual]; // El acceso de esta manera no se encuentra en la imagen pero supongo que esta bien
cant_consumido[post_actual]++;
if (cant_consumido[post_actual] == n)
V(depositar);
V(retirar[post_actual]);
post_actual := (post_actual + 1) mod n;
}
}🧩 Supuestos del ejemplo
tamBuffer = 2→ hay dos slots:buffer[0]ybuffer[1]n = 2→ hay dos consumidores:C1yC2buffer[i]contiene datos generados por el productor- Cada dato debe ser consumido por ambos consumidores antes de poder sobrescribir el slot
- Los consumidores deben leer los datos en orden
🔁 Estado inicial
| Variable / Recurso | Valor inicial |
|---|---|
buffer | [_, _] |
cant_consumido[0] | 0 |
cant_consumido[1] | 0 |
retirar[0], retirar[1] | 1 |
consumir[1], consumir[2] | 0 (esperando dato) |
posLibre (productor) | 0 |
post_actual (consumidores) | 0 |
⏱ Paso 1: El productor genera el primer dato
P(depositar)→ OKbuffer[0] := generarDato() → 10cant_consumido[0] := 0V(consumir[1]),V(consumir[2])posLibre := 1(próximo slot)
⏱ Paso 2: Ambos consumidores empiezan a consumir buffer[0] (dato 10)
Consumer 1:
P(consumir[1])P(retirar[0])→ OKdato := buffer[0] → 10cant_consumido[0] := 1V(retirar[0])(libera acceso al slot)post_actual := 1
Consumer 2:
P(consumir[2])P(retirar[0])→ OKdato := buffer[0] → 10cant_consumido[0] := 2cant_consumido[0] == n→V(depositar)→ libera al productorV(retirar[0])post_actual := 1
⏱ Paso 3: El productor genera el segundo dato
P(depositar)→ OK (fue liberado)buffer[1] := generarDato() → 20cant_consumido[1] := 0V(consumir[1]),V(consumir[2])posLibre := 0
⏱ Paso 4: Ambos consumidores consumen buffer[1] (dato 20)
Consumer 1:
P(consumir[1])P(retirar[1])dato := buffer[1] → 20cant_consumido[1] := 1V(retirar[1])post_actual := 0
Consumer 2:
P(consumir[2])P(retirar[1])dato := buffer[1] → 20cant_consumido[1] := 2V(depositar)(productor puede continuar)V(retirar[1])post_actual := 0
🔁 Y así continúa el ciclo…
✅ Propiedades garantizadas
| Propiedad | ¿Cumple? |
|---|---|
| Exclusión mutua en el buffer por slot | ✅ |
| Orden de consumo por slot | ✅ |
| Reutilización del slot solo tras n lecturas | ✅ |
| Independencia de tiempo entre consumidores | ✅ |
| Fairness (todos acceden eventualmente) | ✅ |
8) Implemente una butterfly barrier para 8 procesos#
Implemente una butterfly barrier para 8 procesos usando variables compartidas.
Respuesta
Una butterfly barrier tiene log2(n) etapas.
Cada Worker sincroniza con un Worker distinto en cada etapa.
En particular, en la etapa s un Worker sincroniza con un Worker a distancia 2^(s-1).
Se usan distintas variables flag para cada barrera de dos procesos.
Cuando cada Worker pasó a través de log2(n) etapas, todos los Workers deben haber arribado a la barrera y por lo tanto todos pueden seguir.
Esto es porque cada Worker ha sincronizado directa o indirectamente con cada uno de los otros.
Diagrama (sincronizaciones por etapa)
Workers 1 2 3 4 5 6 7 8
Etapa 1 └───┘ └───┘ └───┘ └───┘
Etapa 2 └─────────┘ └─────────┘
Etapa 3 └───────────────────────┘Codigo
int N = 8;
int E = log(N);
int arribo[1:N] = ([N] 0);
process Worker[i = 1 to N] {
int j;
int resto;
int distancia;
while (true) {
// Sección de código anterior a la barrera.
// --- Inicio de la barrera butterfly ---
for (etapa = 1; etapa <= E; etapa++) {
distancia = 2 ^ (etapa - 1); // distancia = 2^(etapa-1)
resto = i mod 2 ^ etapa;
if (resto == 0 || resto > distancia) // define si sincroniza con i+dist o i-dist
distancia = -distancia;
j = i + distancia;
while (arribo[i] == 1) skip; // espera a que su flag esté en 0
arribo[i] = 1; // indica que llegó
while (arribo[j] == 0) skip; // espera a su par
arribo[j] = 0; // limpia la flag del otro
}
// --- Fin de la barrera butterfly ---
// Sección de código posterior a la barrera.
}
}Este no me quedo del todo claro pero bueno
9) Suponga n^2 procesos organizados en forma de grilla cuadrada#
Suponga n^2 procesos organizados en forma de grilla cuadrada. Cada proceso puede comunicarse solo con los vecinos izquierdo, derecho, de arriba y de abajo (los procesos de las esquinas tienen solo 2 vecinos, y los otros en los bordes de la grilla tienen 3 vecinos). Cada proceso tiene inicialmente un valor local v.
a) Escriba un algoritmo heartbeat que calcule el máximo y el mínimo de los n2 valores. Al terminar el programa, cada proceso debe conocer ambos valores. (Nota: no es necesario que el algoritmo esté optimizado).
Respuesta
Chan valores[1:n; 1:n](int);
Process P[i = 1 to n, j = 1 to n] {
Int v;
Int Nuevo, minimo = v, maximo = v;
Int cantVecinos;
Vecinos[1..cantVecinos];
For (k = 1 to cantGeneraciones) {
For (p = 1 to cantVecinos) {
Send valores[vecinos[p].fila, vecinos[p].columna](v);
}
For (p = 1 to cantVecinos) {
Receive valores[i, j](nuevo);
if (nuevo < minimo)
minimo = nuevo;
if (nuevo > maximo)
maximo = nuevo;
}
}
}🎯 Supongamos 3 procesos: A, B, C
A --- B --- C- A tiene valor 5
- B tiene valor 2
- C tiene valor 8
Cada uno está conectado con sus vecinos inmediatos.
🧪 Generación 1: Intercambio de valores
-
- A envía 5 a B
-
- B envía 2 a A y C
-
- C envía 8 a B
[5] [2] [8]
A <--> B <--> C🔍 ¿Qué recibe cada uno?
| Proceso | Recibe de | Valores recibidos | Nuevo mínimo | Nuevo máximo |
|---|---|---|---|---|
| A | B | [2] | 2 | 5 |
| B | A, C | [5, 8] | 2 | 8 |
| C | B | [2] | 2 | 8 |
✅ Resultado final (después de 1 ronda)
A: mínimo = 2, máximo = 5
B: mínimo = 2, máximo = 8
C: mínimo = 2, máximo = 8Si hacemos otra ronda, A también recibirá el 8 (a través de B), y entonces todos tendrán:
mínimo = 2, máximo = 8📌 Esto mismo pasa en grillas grandes: con varias generaciones, los valores extremos se difunden.
b) Analice la solución desde el punto de vista del número de mensajes.
Respuesta
En cada ronda, los procesos envían mensajes a sus vecinos. Dependiendo de su posición en la grilla, cada proceso tiene distinta cantidad de vecinos:
🔹 Esquinas (4 procesos)
-
Cada uno tiene 2 vecinos → envía 2 mensajes por ronda
-
Total por todas las rondas:
plaintext4 procesos * 2 mensajes * (n-1) rondas * 2 (envío y recepción) = 4 * 2 * (n - 1) * 2 = (n - 1) * 16 mensajes
🔹 Bordes (sin esquinas) → hay 4 lados con (n - 2) procesos cada uno
-
Cada uno tiene 3 vecinos → envía 3 mensajes por ronda
-
Total:
plaintext(n - 2) * 4 procesos * 3 mensajes * (n - 1) rondas * 2 = (n - 2) * 4 * 3 * (n - 1) * 2 = (n - 1)(n - 2) * 12 mensajes
🔹 Internos → (n - 2) × (n - 2) procesos
-
Cada uno tiene 4 vecinos → envía 4 mensajes por ronda
-
Total:
plaintext(n - 2)^2 * 4 mensajes * (n - 1) rondas * 2 = (n - 2)^2 * (n - 1) * 8 mensajes
Este punto se podria mejorar
c) ¿Puede realizar alguna mejora para reducir el número de mensajes?
Respuesta
No, no es posible reducir el número de mensajes, ya que no existe una forma de saber con certeza cuándo un proceso ha recibido el valor mínimo o máximo global.
Por lo tanto, para garantizar que todos los procesos lleguen a conocer los valores extremos, es necesario ejecutar las (n - 1) × 2 generaciones completas.
Voy a rezar por que no tomen esta wea
Preguntas Teoricas Comunes#

Pregunta 1 Ventajas y Desventajas#
3- Defina los paradigmas de interacción entre procesos distribuidos token passing, servidores replicados y prueba-eco. Marque ventajas y desventajas en cada uno de ellos cuando se utiliza comunicación por mensajes sincrónicos o asincrónicos.
Token Passing
Es un esquema donde un mensaje especial (token) circula entre los procesos. Solo el que tiene el token puede ejecutar una acción crítica, como entrar a la sección crítica o tomar decisiones.
Ejemplo: exclusión mutua distribuida, detección de terminación.
Ventajas: simple de implementar, no necesita reloj ni identificadores globales, funciona bien en topologías como anillo.
Desventajas: si se pierde el token el sistema se bloquea; no hay paralelismo (solo trabaja quien tiene el token); puede haber demoras innecesarias.
Mejor comunicación: asincrónica, porque permite circulación sin bloqueo. Se adapta bien a arquitecturas de memoria distribuida (AMP).
Servidores Replicados
Varios procesos replican un recurso compartido (archivo, base de datos) para brindar alta disponibilidad y tolerancia a fallos. A los clientes les parece que hay un único servidor.
Ejemplo: mozos en el problema de los filósofos, sistemas de archivos distribuidos.
Ventajas: mayor disponibilidad, tolerancia a fallos, mejora el rendimiento si se balancean bien los pedidos.
Desventajas: mantener la consistencia entre réplicas es complejo; puede haber conflictos si dos servidores procesan escrituras en paralelo.
Mejor comunicación: asincrónica (evita bloquear al cliente), ideal en AMP. En SMP es más difícil porque hay que mantener varios canales y controlarlos.
Prueba-Eco
Un nodo envía mensajes “probe” a sus vecinos; cuando todos responden con “eco”, el emisor sabe que se llegó a todos. Sirve para explorar redes desconocidas o detectar nodos activos.
Ejemplo: descubrimiento de topología en redes móviles o dinámicas.
Ventajas: útil sin conocer la red; robusto frente a cambios; permite diseminar o recolectar información.
Desventajas: puede generar muchos mensajes; necesita control para evitar ciclos o duplicación.
Mejor comunicación: asincrónica, ideal en AMP por su descentralización y tolerancia a variaciones en la red.
Finales#


















